机器学习系列笔记

2026-01-16    #机器学习  

声明：个人学习笔记

一、决策树

决策树（decision tree）是一类常见的机器学习（分类）方法，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策树对新数据进行分析。

1. 决策树的模型与学习

1.1 简单的例子：选西瓜的一棵决策树

一般，一颗决策树包含一个根节点（node），若干个内部结点（internal node）和若干个叶节点（leaf node）；叶节点对应于决策结果，其他每个结点对应于一个属性测试；每个结点包含的样本的集合根据属性测试的结果被划分到子节点中。

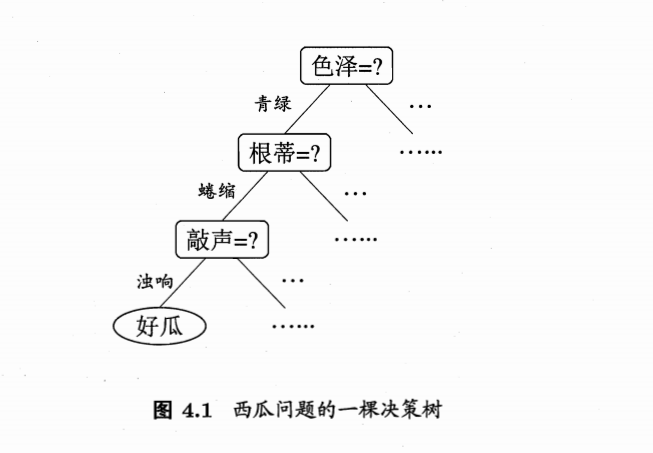
选择西瓜的决策树

在沿着决策树从上到下的遍历过程中，在每个结点都有一个测试。对每个结点上问题的不同测试输出导致不同的分支，最后会达到一个叶子结点。这一过程就是利用决策树进行分类的过程，利用若干个变量来判断属性的类别。

1.2 决策树模型

决策树（decision tree）是一类常见的机器学习（分类）方法，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策树对新数据进行分析。

决策树本质上是从训练数据集中归纳出一组分类规则，决策树学习通常包括三个步骤：特征选择、决策树生成和决策树修剪。

1.3 决策树和归纳算法

从特殊的训练样例中归纳出一般函数是机器学习的核心问题，从训练样例中进行学习的过程：

1. 训练集D={(x1,y1), (x2,y2),…,(xn,yn)}，属性集A={a1,a2,…,av}

2. 学习过程将进行对目标函数f的不断逼近，每一次逼近都叫做一个假设h

3. 假设需要以某种形式进行，如 y=ax+b。通过调整假设的表示，即应用不同算法，产生出假设的不同变形

4. 从不同的变形中选择最佳的组合

1.4 选择方法

使训练值与假设值预测出的值之间的误差平方和 Err 最小

$$min err = \sum_{i=0}^n(\hat{y}_i - y_i)^2 $$

1.5 决策树算法

2. 特征选择

决策的关键在于如何选择最优划分属性一般而言，随着划分过程不断进行，决策树分支结点所包含的样本尽可能属于同一类别，即“纯度”越来越高。通常特征选择的准则是信息增益（information gain）或信息增益比(gain ratio)。

2.1 信息熵（Entropy）

三十而立，四十而不惑，五十知天命…人生，就是一次熵不断变小的过程。

香农 1948 年提出信息论理论，在信息论和概率统计中，熵（entropy）是表示随机变量不确定性的度量，用来度量样本集合纯度最常用的一些指标。样本集合 D 中第 k 类样本所占比例为 pk（k=1,2,…,|y|），则 D 的信息熵定义为：

$$H(D)=-\sum_{k=1}^{|y|}{p_klog_2{p_k}}$$

熵越大，随机变量的不确定性越大。当 D 服从 0,1 分布时，熵与不确定性程度的关系：

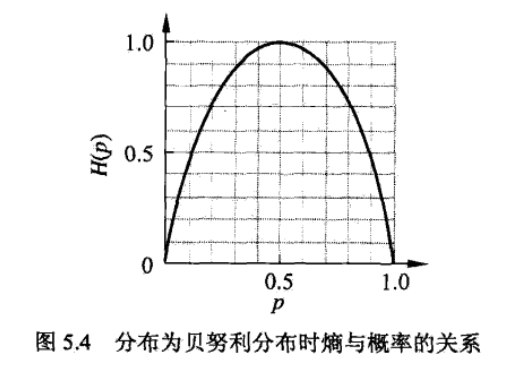
熵与不确定性程度的关系

如图，当 p 为 0 或 1 时，熵值最小，随机变量完全没有不确定性，当 p=0.5 时，熵值达到最大值，随机变量的不确定性最大。

2.2 信息增益（Information gain）

假定离散属性 a 有 V 个可能的取值 {a1,a2,…,aV}，使用 a 对样本集进行划分，则会产生 V 个分支结点，其中第 v 个分支结点包含了 D 中所有在属性 a 上取值为 av 的样本，记为 Dv，于是可以计算出属性 a 对样本集 D 进行划分所获得的信息增益（information gain）：

$$Gain(D,a)=H(D)-\sum_{v=1}^{V}\frac{|D^v|}{|D|}H(D^v)$$

信息增益表示得知属性 a 的信息而使得 D 的信息不确定性减少的程度，决策树学习中的信息增益等价于训练数据集中划分属性与类别的互信息（mutual information）。

2.3 信息增益率（Gain ratio）

著名的 C4.5 决策树算法不直接使用信息增益，而是使用信息增益率（gain ratio）来选择最优划分属性，增益率定义为：

$$Gain_{Ratio}=\frac{Gain(D,a)}{IV(a)}$$

$$IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_2{\frac{D^v}{|D|}}$$

IV(a) 称为 a 属性的“固有值”(intrinsic value)，所以一般增益率准则对数目较少的属性有所偏好。如果 av 属性的数目越大，IV(a) 相应也会变大，所以比较其增益就没有太大优势。举个例子，如果需要你选择一个特征来划分人群，身份证号码是一个完美的选择，但是我们并不能在实际中应用这个特征。选择信息增益率来做特征选择就是为了避免出现这种状况，我们不仅仅要考量特征对数据的划分能力，而且还需要考察特征本身的信息熵。

2.4 基尼指数（Gini index）

CART 决策树使用基尼指数来选择划分属性，数据集 D 的纯度可以用基尼值来度量：

Gini(D) 反映了从数据集中随机抽取两个样本，其类别标记不一致的概率，因此 Gini(D) 越小，数据集 D 的纯度越高。

于是，属性集合 A 中，选择使得划分后基尼指数最小的属性作为最优划分属性

3. 决策树的生成

3.1 决策树 ID3 算法

在决策树分类中，假定 D 是训练样本集合，|D| 是训练样本数，离散属性 a 有 V 个可能的取值{a1,a2,…,aV}，使用 a 对样本集进行划分，则会产生 V 个分支结点，其中第v个分支结点包含了 D 中所有在属性 a 上取值为 av 的样本，记为 Dv，于是可以计算出属性 a 对样本集 D 进行划分所获得的信息增益（information gain）：

$$Gain(D,a)=H(D)-{\sum_{v=1}^{V}}{\frac{|D^v|}{|D|}}H(D^v)$$

信息增益表示得知属性 a 的信息而使得 D 的信息不确定性减少的程度。经验条件熵 H(D|A) 表示在特征 A 给定的条件下对数据集 D 进行分类的不确定性，它们的差即信息增益。

3.2 决策树 ID3 算法-流程


输入： 训练数据集D，特征集A，阈值ε；

输出： 决策树T

（1） 若D中所有实例均属于同一类Ck，则T为单节点树，并将Ck>作为该节点的类标记，返回T；

（2） 若A=∅，则T为单节点树，并将D中实例树最大的类Ck作为该节点的类标记，返回T；

（3）否则，按照信息增益的计算方法，选择信息增益最大的特征Ag;

（4）如果的信息增益小于阈值，则置T为单节点树，并将D中实例数最大的类Ck作为该节点的类标记，返回T；

（5）否则，对Ag的每一可能值ai，依Ag=ai将D分割为若干非空子集Di，将中实例最大的类作为标记，构建子结点，由结点及其子节点构成树T，返回T；

（6）对第i个子结点，以Di</sub>为训练集，以A-{Ag}为特征集，递归地调用步（1）~步

（5），得到子树Ti，返回Ti

3.3 ID3 算法-小结

ID3 算法的基本思想是，以信息熵为度量，用于决策树结点的属性选择，每次优先选取信息量最多的属性，构建一棵熵值下降最快的决策树，到叶节点处的熵值为 0。

3.4 决策树 C4.5 生成算法

ID3 算法只有树的生成，所以该算法容易生成的树很容易产生过拟合，从而泛化能力不佳。C4.5 的算法过程与 ID3 类似，只是属性选择的指标换成了信息增益比。

4. Python 实现代码分析

from math import log
import operator

def credataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels           

dataset, labels = credataSet()

labels

    ['no surfacing', 'flippers']

feat = [example[1] for example in dataset]

set(feat)

    {0, 1}

#计算信息熵
def calEnt(dataset): 
    numEnteries = len(dataset) 
    # 新建一个空的字典，这种用法通常用于数据集中字段计数
    labelCounts = {} 
    for featVec in dataset:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1 
    Ent = 0.0
    for key in labelCounts:
        # 先转换为浮点
        prob = float(labelCounts[key]) / numEnteries 
        Ent -= prob * log(prob, 2)
    return Ent

ent = calEnt(dataset)

# 按照指定特征划分数据集
# dataset：待划分的数据集，axis：划分数据集特征
# value：返回的特征的值
def splitDataSet(dataset, axis, value): 
    retDataSet = []
    for featVec in dataset:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

splitdata = splitDataSet(dataset, 0, 1)

splitdata

    [[1, 'yes'], [1, 'yes'], [0, 'no']]

def chooseBestFeatureToSplit(dataset):
    numFeatures = len(dataset[0]) - 1
    baseEntropy = calEnt(dataset)
    bestInfoGain = 0.0; bestFeature = -1 
    for i in range(numFeatures): 
        # 取每一个样本的第i+1个元素，featList = [1, 1, 0, 1, 1]
        # set(featList) = {0,1}，set是得到列表中唯一元素值的最快方法
        featList = [example[i] for example in dataset] 
        uniqueVals = set(featList) 
        newEntropy = 0.0
        for value in uniqueVals:
            # 遍历特征下属性值，对每一个属性值划分一次数据集
            subDataSet = splitDataSet(dataset, i, value) 
            prob = len(subDataSet)/float(len(dataset)) 
            newEntropy += prob * calEnt(subDataSet)
        # 计算两个特征各自的信息增益，并进行比较
        infoGain = baseEntropy - newEntropy 
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

bestfeature = chooseBestFeatureToSplit(dataset)

majorityCnt(classList) 函数使用分类名称的列表然后创建值为 classList 中唯一值的数据字典，字典对象存储了 classList 中每个类标签出现的频率，最后利用 operator 操作键值排序字典，并返回出现次数最多的分类名称。

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys(): classCount[Vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataset, labels):
    classList = [example[-1] for example in dataset]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 如果数据的长度为1，那么意味着所有的特征都用完了，分类完毕并返回次数最多的分类名称
    if len(dataset[0]) == 1: 
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataset)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    # 当dataset的特征被选中为bestFeat后便不再作为候选划分特征，所以要删除掉
    del(labels[bestFeat]) 
    featValues = [example[bestFeat] for example in dataset]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataset, bestFeat, value), subLabels)
    return myTree

createTree(dataset, labels)

    {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

二、线性回归

1. 基本形式

给定 d 个属性 $x=(x_1;x_2;\cdots;x_d)$，线性模型（linear model）可以表示为一个试图通过属性的线性组合来进行预测的函数：

$$f(x)=w^Tx+b$$

其中，$x_i$ 表示属性 $x$ 在第 $i$ 个属性上的取值，$w$ 直观表达了各个属性在模型预测中的重要性，$w=(w_1;w_2;\cdots;w_d)$。那么，如何求得 $w$ 和 $b$ 便成为了线性回归的主要任务。

2. 误差度量（Error Measure）

给定数据集 $D={(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)}$，其中 $x_i=(x_{i1};x_{i2};\cdots;x_{id})$，$y_i\in\mathbb{R}$。假设有 $d$ 个属性，线性回归的目标是学得：

$$f(x_i)=wx_i+b$$

使得 $f(x_i)\approx{y_i}$。均方误差是回归任务中最常用的性能度量，因此可以通过让均方误差最小化得到拟合参数

$$(w^,b^)={argmin}\sum_{i=1}^m(f(x_i)-y_i))^2$$

3. 拟合参数

我们可以利用最小二乘法来对 $w$ 和 $b$ 进行估计。为了计算方便，我们将权重和偏置项合并为一个向量 $\hat{w}$，维度为（d+1）×1。相应的，将数据集 $D$ 表示为 m×（d+1）大小的矩阵 $\mathtt{X}$，其中每一行代表一个示例，最后一个元素恒为 1，即

$$\mathtt{X}= \begin{bmatrix} {x_{11}}&{x_{12}}&{\cdots}&{x_{1d}}&{1}\ {x_{21}}&{x_{22}}&{\cdots}&{x_{21}}&{1}\ {\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\ {x_{m1}}&{x_{m1}}&{\cdots}&{x_{md}}&{1}\ \end{bmatrix}$$

标记值记为 $y$，运用最小二乘法(Ordinary Least Square)来估计参数

$$E_{\hat{w}^*}=argmin{(y-{\mathtt{X}}{\hat{w}})}^T(y-{\mathtt{X}}{\hat{w}})$$

对 $\hat{w}$ 求导得到

$$\frac{\partial{E_{\hat{w}}}}{\partial{\hat{w}}}=2\mathtt{X}^T(\mathtt{X}\hat{w}-y)$$

令上式为零便可得 $\hat{w}$ 的最优解

$${\hat{w}}^*={({\mathtt{X}}^T{\mathtt{X}})}^{-1}{\mathtt{X}}^Ty$$

最终，学到的多元线性回归模型为

$$f({\hat{x}}i)={\hat{x}}{i}^T{({\mathtt{X}}^T{\mathtt{X}})}^{-1}{\mathtt{X}}^Ty$$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression


def plot_linear_regression():
    a = 0.5
    b = 1.0

    # x from 0 to 10
    x = 30 * np.random.random(20)

    # y = a*x + b with noise
    y = a * x + b + np.random.normal(size=x.shape)

    # create a linear regression classifier
    clf = LinearRegression()
    clf.fit(x[:, None], y)

    # predict y from the data
    x_new = np.linspace(0, 30, 100)
    y_new = clf.predict(x_new[:, None])

    # plot the results
    ax = plt.axes()
    ax.scatter(x, y)
    ax.plot(x_new, y_new)

    ax.set_xlabel('x')
    ax.set_ylabel('y')

    ax.axis('tight')


if __name__ == '__main__':
    plot_linear_regression()
    plt.show()

拟合

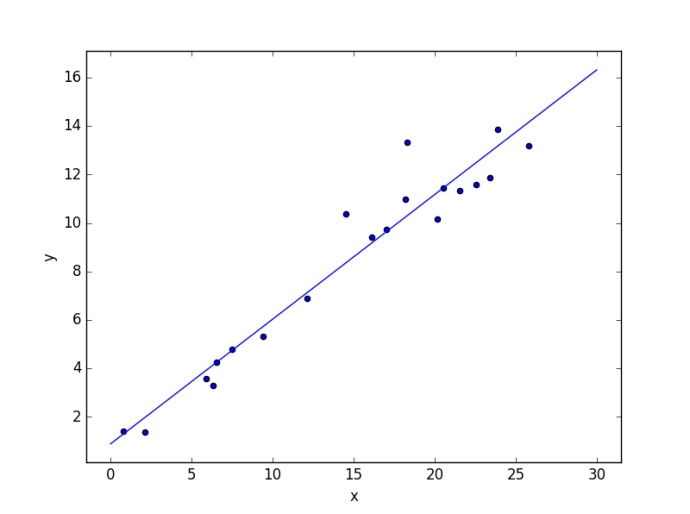
三、Logistic Regression

上一篇文章讲到了线性模型，线性模型形式十分简单，却有丰富的变化。一般线性模型有一定的缺陷，那就是 $y=w^T x+b$ 的预测值是为数值型的，当面对要求预测值为离散型就有些力不从心了，它会很容易受到异常值的影响，从而导致误差。那么，可不可以令预测值 $y$ 变成另外一种形式呢？比如，在分类任务里，我们要求预测值为离散型的，得到一个是或否的答案，不再是原来的连续性预测值。这里就要用到机器学习中的一个重要的模型——Logistic Regression，即逻辑斯蒂回归或对数线性回归 (log-linear regression)。

$$ \ln y = w^T x + b $$

实际上是在试图让 $e^{w^T+b}$ 逼近 $y$，形式上仍然是线性回归，但实质上是在求线性空间到非线性空间的映射。

目录

1. Logistic 分布

在学习 Logistic Regression 之前，我们有必要了解一下 Logistic 分布函数和密度函数：

$$ F(x) = P(X \le x) = \frac{1}{1+e^{-(x-\mu)/\gamma}} $$

$$ f(x) = F’(x) = \frac{e^{-(x-\mu)/\gamma}}{\gamma{(1+e^{-(x-\mu)/\gamma})}^2} $$

式中，$\mu$ 为位置参数，$\gamma \gt 0$ 是形状参数。

逻辑斯蒂函数实际上是线性回归模型的预测结果取逼近真实标记的对数几率，其对应的模型是对数几率回归。

2. Logistic 函数

考虑一个二分类任务，其输出标记为 $y \in {0,1}$，而线性回归模型产生的预测值 $z$ 是实数值，于是我们需要将 $z$ 转换为 0/1 值，理想的方法是对数几率函数：

$$ y = \frac{1}{1+e^{-z}} $$

对数几率函数是一种 “Sigmoid 函数”，它将 $z$ 值转化为一个接近 0 或 1 的 $y$ 值，并且输出值在 $z=0$ 附近的变化很陡峭，若预测值大于零就判为正例，小于零就判为反例，预测值为临界值零则可任意判别。

如果我们将线性模型 $z=w^T x+b$ 代入上式，得：

$$ y = \frac{1}{1+e^{-(w^T x+b)}} $$

变形：

$$ \ln \frac{y}{1-y} = w^T x + b $$

若将 $y$ 视为 $x$ 作为正例的可能性，$1-y$ 视为反例的可能性，两者的比值称为 “对数几率” (logit odds)，反映了 $x$ 作为正例的可能性。

由此可以看出，实际上是在用线性回归的模型的预测结果去逼近真实标记的对数几率，因此其对应的模型也被称为 “对数几率回归” (Logistic Regression)。

3. 极大似然估计 (MLE)

类似线性回归，我们需要定义一个损失函数 (loss function)，然后通过最小化损失函数来训练出一个分类器，对于 Logistic Regression，哪种损失函数表现最好？假设选用 0-1 损失函数，考虑 1000 个样本，用训练得到的分类器分类，960 个被分在了正确的一类，其余 40 个划分错误，那么这里损失函数的大小就是 40。考虑调整 $w$ 的大小，得到的损失函数值可能仍然是相同的，没有可以优化的空间。

0-1 损失函数看来是行不通，不妨看看 log 损失函数，为什么选择 log 损失函数？考虑 $-\log(x)$ 函数图像，这个函数图像在趋近于 0 的地方函数值趋于无穷大。相比 0-1 损失函数，它的惩罚性能实在太好，考虑公式（10），假设预测值 $h_w(x^{(i)})$ 为 1，而实际标签 $y^{(i)}$ 为 0，结果便是损失函数会变得很大。并且它的损失函数还是凸函数，存在可优化的空间。

由 Logistic 函数，建立如下表达式：

$$ h_w(x) = g(w^T x) = \frac{1}{1+e^{-w^T x}} $$

根据前文，$p(y=1|x)$ 为正例的概率 $y$，解之，显然有：

$$ \begin{aligned} p(y=1|x) &= h_w(x) \ p(y=0|x) &= 1-h_w(x) \ p(y|x) &= {h_w(x)}^y{(1-h_w(x))}^{1-y}, \quad y=0, 1 \end{aligned} $$

于是，我们可以通过极大似然估计法 (maximum likelihood method) 来估计 $w$（为了计算的方便，将偏置项 $b$ 的权重设为 1，记为 $w_0$）。

给定数据集 ${(x_i,y_i)}_{i=1}^m$，写出对应极大似然函数：

$$ \begin{aligned} L(w) &= \prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta) \ &= \prod_{i=1}^{m}h_w{(x^{(i)})}^{y^{(i)}}{(1-h_w(x^{(i)}))}^{1-y^{(i)}} \end{aligned} $$

再对两边取对数：

$$ \log L(w) = \sum_{i=1}^{m} \left[ y^{(i)} \log h_w(x^{(i)}) + (1-y^{(i)}) \log(1-h_w(x^{(i)})) \right] $$

因此最优解可以通过最大化负的似然函数得到：

$$ \begin{aligned} J(w) &= -\frac{1}{m}\sum_{i=1}^{m} \left[ y^{(i)} \log h_w(x^{(i)}) + (1-y^{(i)}) \log(1-h_w(x^{(i)})) \right] \ J(w) &= -\frac{1}{m}\sum_{i=1}^{m} \left[ y^{(i)} \log \frac{h_w(x^{(i)})}{1-h_w(x^{(i)})} + \log(1-h_w(x^{(i)})) \right] \ J(w) &= -\frac{1}{m}\sum_{i=1}^{m} \left[ y^{(i)}(w^T x) - \log(1+e^{w^T x}) \right] \end{aligned} $$

4. 梯度下降算法 (Gradient Descent)

上式中 $J(w)$ 是一个关于 $\theta$ 的高阶可导连续凸函数，根据凸优化理论，采用梯度下降法求最优解，令 $\theta=(w,b), \min J(\theta)$：

$$ {\theta}_j := {\theta}_j - \alpha \frac{\partial}{\partial{\theta}_j} J(\theta) $$

其中，$\frac{\partial}{\partial{\theta}j}J(\theta)=\frac{1}{m}\sum{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$，$\alpha$ 是步长，当然经过化简之后，上式对 $w$ 的求导是很方便的。

推导过程如下，分部求导。$h(w)$ 对 $w$ 求导的结果是 $-h(w)(1-h(w))x$

$$ \begin{aligned} \frac{\partial}{\partial{w}_j}J(w) &= \frac{\partial{J(w)}}{\partial{h_w(x)}} \cdot \frac{\partial{h_w(x)}}{\partial{w}j} \ &= \left[ y^{(i)} + \frac{y^{(i)}-1}{1-h_w(x^{(i)})} \right] \cdot [h_w(x^{(i)})(1-h_w(x^{(i)}))] x^{(i)} \ &= [y^{(i)}h_w(x^{(i)})(1-h_w(x^{(i)})) + h_w(x^{(i)}(1-y^{(i)}))] \cdot x^{(i)} \ &= (h{w}(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \end{aligned} $$

总的来说，Logistic Regression 是一类比较简单的分类算法，可以把它看做是一类广义线性模型，即线性模型的延伸即可。Logistic Regression 能够很好地胜任二分类问题，Logistic Regression 中关键的问题在于参数优化，传统的 0-1 损失函数非凸，我们不能对其进行优化以得到一个较优参数，log 损失函数是一个不错的选择，它使得损失函数呈凸函数形状（本身并非平方损失函数），这就让梯度下降算法有了施展的空间。

5. Python 代码实现 LR 及分析

from numpy import *
import numpy as np
import matplotlib.pyplot as plt

# 加载数据集，loadDataSet() 函数的主要功能是打开文本文件，并逐行读取；
# 每行的前两列分别为 X1, X2，除此以外，还为偏置项设置一列 X0
def loadDataSet():
    data = []
    label = []
    fr = open('E:/Python/data/testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        data.append([1.0, float(lineArr[0]), float(lineArr[1])])
        label.append(int(lineArr[2]))
    return data, label

data, label = loadDataSet()

# 定义 sigmoid 函数
def sigmoid(z):
    return 1.0 / (1 + exp(-z))

# 定义梯度下降算法
# 设定步长 alpha 为 0.001，迭代次数为 500 次，初始权重 theta 为长度为 n 个值全为 1 的向量
def gradDscent(data, label):
    dataMatrix = np.matrix(data)
    labelMatrix = np.matrix(label).T
    m, n = shape(dataMatrix)
    alpha = 0.001
    iters = 500
    theta = ones((n, 1))
    for k in range(iters):
        # 梯度下降算法，因为要求损失函数的最小值
        # 对应公式（12）
        h = sigmoid(dataMatrix * theta)
        error = (h - labelMatrix)
        theta = theta - alpha * dataMatrix.T * error
    return theta

theta = gradDscent(data, label)
theta = array(theta)
dataArr = array(data)

# 画出决策边界
def plotfit(theta):
    n = dataArr.shape[0]
    x1 = []; y1 = []
    x2 = []; y2 = []
    for i in range(n):
        if int(label[i]) == 1:
            x1.append(dataArr[i, 1])
            y1.append(dataArr[i, 2])
        else:
            x2.append(dataArr[i, 1])
            y2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(x1, y1, s=30, c='red', marker='o')
    ax.scatter(x2, y2, s=30, c='blue', marker='x')
    # 创建等差数列，设定 x 的取值范围为 -3.0 到 3.0
    x = arange(-3.0, 3.0, 0.1)
    y = (-theta[0] - theta[1] * x) / theta[2]
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

plotfit(theta)

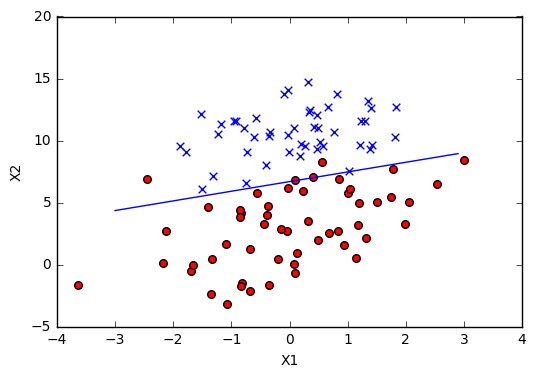
迭代500次之后得到的拟合曲线

分类的结果看起来还不错，从图上看，只有 4 个点被错分。

6. 继续优化：随机梯度下降（SGD）

梯度下降算法在每次更新系数时都需要遍历整个数据集，这样就带来了训练速度变慢的问题，改进的办法是每一次只用一个样本点来更新回归系数，这样的办法被称为随机梯度下降算法。不同于梯度下降算法，在随机梯度下降算法中，

def stoGradDscent0(dataMatrix, labelMatrix):
    m, n = shape(dataMatrix)
    alpha = mat([0.01])
    theta = mat(ones(n)) 
    for i in range(n):
        h = sigmoid(sum(dataMatrix[i] * theta.T))
        error =  h - labelMatrix[i]
        theta = theta - alpha * error * dataMatrix[i]
    return theta

theta = stoGradDscent0(data, label)

def plotfit1(theta):
    import matplotlib.pyplot as plt
    import numpy as np
    dataArr = array(dataMatrix)
    n = dataArr.shape[0]
    x1 = []; y1 = []
    x2 = []; y2 = []
    for i in range(n):
        if int(label[i]) == 1:
            x1.append(dataArr[i, 1])
            y1.append(dataArr[i, 2])
        else:
            x2.append(dataArr[i, 1])
            y2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(x1, y1, s=30, c='red', marker='o')
    ax.scatter(x2, y2, s=30, c='blue', marker='x')
    x = arange(-3.0, 3.0, 0.1)  # 创建等差数列
    y = (-theta[0, 0] - theta[0, 1] * x) / theta[0, 2]
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

plotfit1(theta)

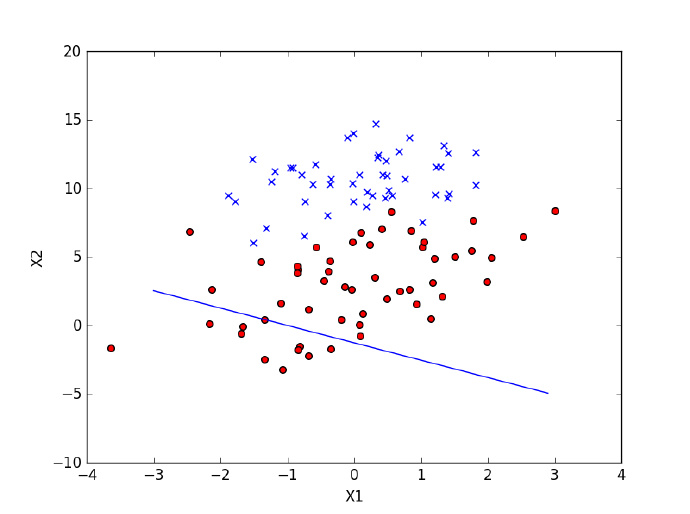
第一次优化的效果不佳，有差不多三分之一的点被误分类，为此进行第二次算法优化：

def stoGradDscent1(dataMatrix, labelMatrix, iters=150):
    m, n = shape(dataMatrix)
    theta = mat(ones(n))
    for j in range(iters):
        dataIndex = list(range(m))  # m = 100
        for i in range(m):
            # 因为 alpha 在每次迭代的时候都会调整，这可以缓解数据的波动，alpha 会减小，但不会到零
            # 通过随机选取样本来更新回归系数，这种方法可以减少周期性的波动
            # uniform() 方法将随机生成下一个实数，它在 [x,y] 范围内
            alpha = 4 / (1.0 + j + i) + 0.01
            randIndex = int(random.uniform(0, len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex] * theta.T))
            error = h - label[randIndex]
            theta = theta - alpha * error * dataMatrix[randIndex]
            # del(dataIndex[randIndex]) 
    return theta

theta = stoGradDscent1(dataMatrix, labelMatrix, iters=150)
print(theta)

plotfit1(theta)

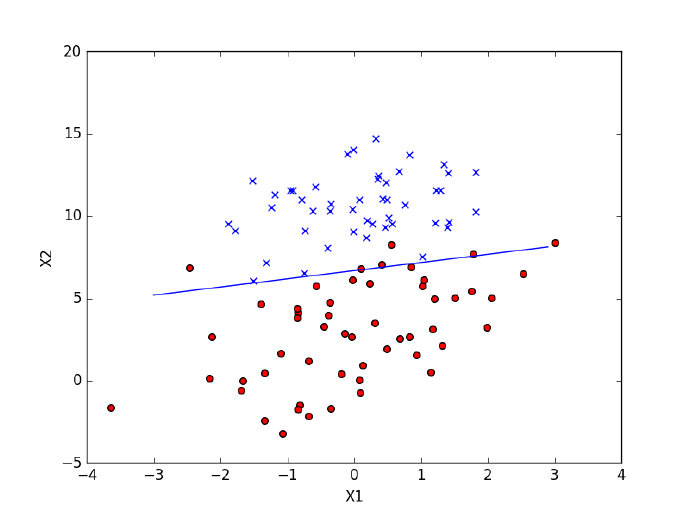
优化参数后的算法可以明显看出分类效果提升了不少，仅仅只有两个点被误分类。

关于 Logistic Regression 的讨论

  1. 为什么 LR 模型要使用 Sigmoid 函数？

    最大熵原理是概率模型学习的一个准则，最大熵原理认为，熵最大的模型是最好的模型。

  2. 逻辑斯蒂回归？

    Logistic Regression 中文翻译为 “逻辑斯谛回归”，梳理了一下周志华老师在微博上的叙述，整理如下：Logistic Regression 与中文的 “逻辑” 没有半点关系，不是 logic，而是 logit，logistic 大概的意思是 “logit 的”，而不是 “log 的”，所以周老师将 Logistic Regression 翻译为对数几率回归。感兴趣的同学可以继续阅读这篇文章：趣谈 “logistic”：物流？后勤？还是 “逻辑斯谛”？

  3. 逻辑回归如何进行多分类？

    如果我们要用逻辑回归进行多分类任务，那么权重矩阵不再是 $m \times 1$，而是 $m \times n$，并且需要用到 softmax 函数来进行归一化。softmax 函数能将 $k$ 维数组中的元素压缩到 0-1 之间，并且所有元素的和为 1，所以考虑到逻辑回归的输出实际上是该分类的可能性估计，对于多分类问题，sigmoid 函数无法将多分类的输出映射到 0-1 之间，而 softmax 正好可以满足这个要求。

    假设现有一个 $K$ 类的数据集，我们先模拟二分类时的处理办法，设第 $K$ 类为主要类别，所有前 $K-1$ 类为次要类别，由公式（6）：

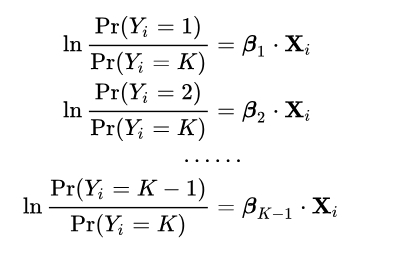
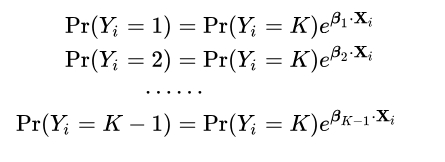
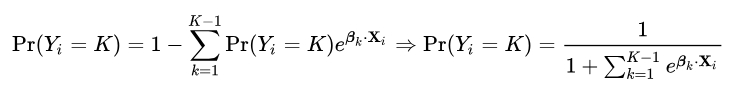
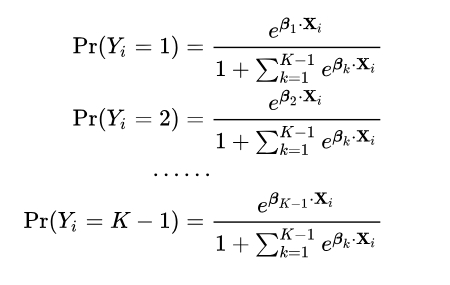
四、支持向量机（上）

在了解支持向量机 (Support Vector Machine, SVM) 之前，你可能会对这个算法的名字感到很奇怪，“支持”？“Machine”？这到底是啥？没错，你不是一个人，一开始的时候我也是相当纳闷。所以，在正式记录之前我想举一个简单的例子辅助理解。

比如说下图（原谅我自己懒得画图），你就先别管图中的英文注释，如果在一个平面上随机散落了若干方形和圆形的点，现在希望你在方形点和圆形点之间找出一条最宽的间隔，你也可以把这条间隔想象成为一条宽宽的 “河流”，然后这条宽宽的间隔又恰好能把河两岸的方形点和圆形点区分开来。

如果把以上的例子看作是分类问题，你会发现跟逻辑回归处理的分类问题思路有区别，逻辑回归会输出一个预测值，然后我们可以通过比较预测值和阈值来确定输出的种类，它属于线性分类器。而刚刚例子中用到的分类方法显然跟逻辑回归是有区别的，它属于非线性的分类器的方法，而这正是支持向量机思想的核心，就是找到一条能把不同点区分开来的宽宽的间隔。

看得出来，上面例子中给的数据是线性可分的，我们可以学习一个线性的分类器，即线性可分支持向量机；当然，现实中的数据不会像例子中的那么完美，当数据是近似线性可分的时候，也可以学习一个线性的分类器，即线性支持向量机；当训练的数据不可分的时候则需要学习非线性支持向量机。伴随着数据越来越复杂，支持向量机的学习方法是从简单到复杂的过程，下面我们来讨论最简单的情形：线性可分支持向量机。

1. 线性可分支持向量机原始问题

支持向量机 (Support Vector Machine, SVM) 是一种分类模型，它的任务是在特征空间上找到正确划分数据集的间隔，并且能使几何间隔最大的分离超平面，简而言之，就是要找到一个平面，能够将空间中的点隔开！

首先，回顾中学时代几何中提到的点到直线的距离 计算方法 ：如果我们通过线性方程 $w^T x+b=0$ 来表示空间中的一条直线，将其记为 $(w,b)$。那么空间中任意一点 $(x_i,y_i)$ 到该直线 $(w,b)$ 的几何距离可以表示为：

$$ d = \frac{|w^T x_i+b|}{||w||} $$

前面我们提到过 SVM 的核心思想是在空间中找到正确划分数据的间隔，并且这个间隔当然越宽越好。

那么如何找到使得间隔最大的分离超平面呢？我们先从最简单的情形开始分析，假设超平面 $w^T x+b=0$ 可以将数据集 100% 正确分类，令：

$$ \begin{cases} w^T x_i + b \ge +1, & \text{为正} \ w^T x_i + b \le -1, & \text{为负} \end{cases} $$

如果我们将可以容忍的间隔设为 1，也就是要求距离该平面 $(w,b)$ 几何距离正负为 1 的空间内没有一个异常点存在，那么寻找最大分离的超平面就意味着上图中两根虚线上的数据点的几何距离 $\frac{2}{||w||}$ 越大越好，转化为数学语言可以表示为如下约束最优化问题：

$$ \begin{aligned} \max_{w,b} \quad & \frac{2}{||w||} \ \text{s.t.} \quad & y_i(w^T x_i + b) \ge 1, \quad i=1,2,\dots,m \end{aligned} $$

在线性可分的情况下，距离分离超平面最近的点称为支持向量，上图中落在虚线上的点就是支持向量，支持向量的决定了分离超平面，一般支持向量的个数不多，往往少数几个训练样本就确定了最终的分离超平面，所以有的时候增加训练样本可能并不会给支持向量机模型的效果带来多少改观。

2. 原始问题转化为对偶问题

我们将线性可分的支持向量机转化为数学语言之后，那么如何求解这个最优化问题呢？

（1）构建拉格朗日函数

该问题的拉格朗日函数可以等价写为（求 $\frac{2}{||w||}$ 的最大值等价于求 $\frac{1}{2}{||w||}^2$ 最小值），$\alpha_i$ 为拉格朗日乘子：

$$ L(w,b,\alpha) = \frac{1}{2}{||w||}^2 - \sum_{i=1}^m \alpha_i (y_i(w^T x_i + b) - 1) $$

这是一个凸二次规划问题，通过拉格朗日乘子法可得到其对偶问题。应用拉格朗日对偶性，原始问题 $(w,b)$ 的对偶问题 $(\alpha)$ 是极大极小问题：

$$ \max \min L(w,b,\alpha) $$

分别令拉格朗日函数对 $w$ 和 $b$ 的偏导数为零可得：

$$ w = \sum_{i=1}^m \alpha_i y_i x_i $$

$$ 0 = \sum_{i=1}^m \alpha_i y_i $$

然后将上述两个式子重新代入拉格朗日函数即可将消去 $w$ 和 $b$：

$$ \begin{aligned} L(w,b,\alpha) &= \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i y_i \left( \left( \sum_{j=1}^{N}\alpha_j y_j x_j \right) x_i + b \right) + \sum_{i=1}^{N}\alpha_i \ &= -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^{N}\alpha_i \end{aligned} $$

然后就得到了原约束问题的对偶问题，即求拉格朗日函数 $L(w,b,\alpha)$ 对 $\alpha$ 的极大：

$$ \begin{aligned} \max_{\alpha} \quad & \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) \ \text{s.t.} \quad & \sum_{i=1}^{N} \alpha_i y_i = 0 \ & \alpha_i \ge 0, \quad i=1,2,\dots,N \end{aligned} $$

故原始问题转化成为了求解对偶问题，为什么要这样做呢？这样做的优点是对偶问题需要求解的参数数量下降，原来需要考虑两个参数 $(w,b)$ ，现在只需要关注 $\alpha$ 便可以了，往往更容易求解。然后可以引入核函数，进而推广到非线性分类问题。设 $\alpha^*$ 是对偶问题的最优化解，那么：

$$ \begin{aligned} w^* &= \sum_{i=1}^m \alpha_i^* y_i x_i \ b^* &= y_j - \sum_{i=1}^{N} \alpha_i^* y_i (x_i \cdot x_j) \end{aligned} $$

求得了 $w^$，$b^$，也就得到了我们需要的分离超平面。

当然这篇文章主要针对的是线性可分问题，那么线性不可分问题以及对偶问题的求解又怎么解决呢？后面的文章将会继续解释。

我把上述拉格朗日乘子法的求解过程用手写了一遍，辅助理解。

拉格朗日乘子法求解

五、支持向量机（中）

在支持向量机（上）我们介绍了线性可分问题的支持向量机方法，不过实际的业务场景中一般不会有那么干净的数据集，有的情况下数据集中的样本是不可分的。但我们要求方法更具有适用性，如果碰到线性不可分问题，我们要适当允许支持向量机容忍一些错误，也就是那条宽宽的 “间隔” 中允许存在无法归类的数据。

1. 硬还是软？

针对近似线性可分的问题，我们要求所谓的间隔中不能有无法归类的数据，这条间隔比较严格，称之为硬间隔。而对于线性不可分的情形，硬间隔最大化的方法就不适用了，因为一旦间隔区域有异常点，硬间隔的不等式约束不一定都成立。对于不能满足函数硬间隔条件的数据集，需要对硬间隔最大化做一些调整，容许有些许的异常点存在，这样的方法叫做软间隔最大化。

回顾硬间隔最大化的约束最优化问题：

$$ \begin{aligned} \max_{w,b} \quad & \frac{2}{||w||} \ \text{s.t.} \quad & y_i(w^T x_i + b) \ge 1, \quad i=1,2,\dots,m \end{aligned} $$

硬间隔最大化的优化问题的约束条件很严格，也就是所有的样本点必须被划分正确。

何谓 “软”？也就是将约束条件放松一点点，有些数据破坏了间隔条件是被容许的，但是也不能太多。我们给约束条件加上一个松弛变量 $\xi_i$，放宽约束条件，这样硬间隔最大化里面要求的间隔强制为 1 的约束条件就变为：

$$ y_i(w x_i + b) \ge 1 - \xi_i $$

同时，对松弛变量加上惩罚参数 $C \gt 0$，惩罚参数的大小控制误分类的容忍程度，目标函数就变为：

$$ \frac{1}{2}{||w||}^2 + C\sum_{i=1}^{N}\xi_i $$

所以线性不可分的支持向量机问题变为凸二次规划问题，我们暂且称为原始问题：

$$ \begin{aligned} \min_{w,b,\xi} \quad & \frac{1}{2}{||w||}^2 + C\sum_{i=1}^{N}\xi_i \ \text{s.t.} \quad & y_i(w x_i + b) \ge 1-\xi_i, \quad i=1,2,\dots,N \ & \xi_i \ge 0, \quad i=1,2,\dots,N \end{aligned} $$

2. 转化为对偶问题

同线性可分的问题求解的分析过程一样，对线性不可分的支持向量机凸二次规划问题，依然选择拉格朗日乘子法求解，然后转化为求解对偶问题。

（1）首先对原始问题构建拉格朗日函数

$\alpha$ 和 $\mu$ 为拉格朗日乘子：

$$ L(w,b,\xi,\alpha,\mu) = \frac{1}{2}{||w||}^2 + C\sum_{i=1}^{N}\xi_i - \sum_{i=1}^{N}\alpha_i (y_i(w x_i + b) - 1 + \xi_i) - \sum_{i=1}^{N}\mu_i \xi_i $$

（2）对偶问题是拉格朗日函数的极大极小问题

先对极小化 $L(w,b,\alpha)$，分别对 $w,b,\xi$ 求偏导并令其等于零：

$$ \begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{N}\alpha_i y_i x_i = 0 \ \frac{\partial L}{\partial b} &= \sum_{i=1}^{N}\alpha_i y_i = 0 \ \frac{\partial L}{\partial \xi} &= C - \alpha_i - \mu_i = 0 \end{aligned} $$

得：

$$ \begin{aligned} w &= \sum_{i=1}^{N}\alpha_i y_i x_i \ \sum_{i=1}^{N}\alpha_i y_i &= 0 \ C - \alpha_i - \mu_i &= 0 \end{aligned} $$

然后将上述三个式子带入拉格朗日函数即可将消去 $w$ 和 $b$，即：

$$ L(w,b,\xi,\alpha,\mu) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j x_i x_j + \sum_{i=1}^{N}\alpha_i $$

对偶问题是拉格朗日函数极大极小问题，求上式对 $\alpha$ 的极大化，即得对偶问题：

$$ \begin{aligned} \max_{\alpha} \quad & -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j x_i x_j + \sum_{i=1}^{N}\alpha_i \ \text{s.t.} \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \ & C - \alpha_i - \mu_i = 0 \ & \alpha_i \ge 0, \mu_i \ge 0, \quad i=1,2,\dots,N \end{aligned} $$

当拉格朗日函数转化为其对偶问题的形式之后，需要求解的参数数量下降了，只需要完成对 $\alpha$ 极大化的求解，原始问题 $w^{},b^{}$ 的解可由下式求得，接下来的任务只需要求解 $\alpha$ 了，如下：

$$ \begin{aligned} w^{} &= \sum_{i=1}^{N} \alpha_i^{} y_i x_i \ b^{} &= y_j - \sum_{i=1}^{N} y_i \alpha_i^{} (x_i \cdot x_j) \end{aligned} $$

3. 非线性支持向量机与核函数

无论是上一篇讨论线性可分和这篇笔记以上讨论线性不可分问题都属于线性分类问题的范畴，有线性分类势必就有非线性分类，比如如下的动图，在做变化之前的确有一个超平面能把红色和蓝色数据分割开，但是这样的求解往往太麻烦了，如果转换一个角度，对数据做一次转换，原有的非线性问题就变成了线性问题了，求解的难度下降了很多。

针对非线性分类问题，我们一般使用非线性支持向量机的方法，其主要特点是核技巧 (kernel trick)。核技巧的基本想法是通过非线性变换将输入空间（一般是欧式空间或离散集合）映射到另一个特征空间，简单一点理解就是函数变换。

$$ \phi(x): x \to \mathcal{H} $$

$$ K(x,z) = \phi(x) \cdot \phi(z) $$

其中 $K(x,z)$ 为核函数，$\phi(x)$ 为映射函数。

因此，当核技巧应用于支持向量机中，对偶问题的目标函数中的内积 $(x_i,x_j)$ 便可以用核函数 $K(x,z)=\phi(x)\cdot\phi(z)$ 来代替，故对偶问题的目标函数变为只有 $\alpha$ 一个参数了：

$$ w(\alpha) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i, x_j) + \sum_{i=1}^{N}\alpha_i $$

对以上问题的求解过程这里就不具体讨论了。

3.1 几种常见的核函数

在实际中，我们经常会碰到非线性的分类问题，为了避免复杂的线性变换，这时需要应用核技巧来将数据从低维空间映射到高维空间，然后再采用线性分类器的学习方法训练模型，关于核函数的解释，知乎上的一个回答非常形象 机器学习有很多关于核函数的说法，核函数的定义和作用是什么？ - 知乎 ，这篇文章也值得阅读 支持向量机: Kernel « Free Mind 。

小结

这篇笔记介绍了软间隔方法和核函数，以及如何将原始问题转化为只有一个参数的对偶问题，这两篇笔记都只提到了如何转换为对偶问题，至于如何求解 $\alpha_i$ 还没有做分析，在接下来的笔记中，我们会学习一种专门对付求解 $\alpha_i$ 的 SMO 算法。

六、支持向量机（下）

前两篇笔记主要记录了在线性可分、线性不可分和非线性可分三种情形下，如何将支持向量机的原始优化问题转化为只有一个参数的对偶问题，对偶问题的求解实现没有记录，这篇笔记讲到的序列最小最优算法 (SMO) 就是一种高效实现支持向量机学习的算法。

由上一篇笔记，凸二次规划的对偶问题：

$$ \begin{aligned} \min \quad & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j K(x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i \ \text{s.t.} \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \ & 0 \le \alpha_i \le C, \quad i=1,2,\dots,N \end{aligned} $$

1. SMO 算法基本思路

不同于之前解决二次规划问题所采取的手段，SMO 选择在每一步解决一个最小可能的优化问题，通过求解子问题来逼近原始问题，这可以大大提高整个算法的计算速度，是一种启发式的方法。SMO 与提升树中的前向分步算法或者 ALS（交替最小二乘法）的思路殊途同归，它们都是通过不断解决小问题来逼近最优解。

SMO 的优势：

  1. Can be done analytically
  2. 不需要额外的矩阵存储空间
  3. SMO = analytic method + heuristic（启发式）

由上述对偶问题，假设先固定除 $\alpha_1, \alpha_2$ 之外的所有其他变量，于是对偶问题的子问题可以等价写为：

$$ \begin{aligned} \min_{\alpha_1, \alpha_2} \quad & \frac{1}{2}K_{11}{\alpha_1}^2 + \frac{1}{2}K_{22}{\alpha_2}^2 + y_1 y_2 K_{12} \alpha_1 \alpha_2 - (\alpha_1 + \alpha_2) + y_1 \alpha_1 \sum_{i=3}^{N} y_i \alpha_i K_{i1} + y_2 \alpha_2 \sum_{i=3}^{N} y_i \alpha_i K_{i2} \ \text{s.t.} \quad & \alpha_1 y_1 + \alpha_2 y_2 = -\sum_{i=3}^{N} y_i \alpha_i = k \ & 0 \le \alpha_i \le C, \quad i=1,2,\dots,N \end{aligned} $$

由对偶问题的约束条件 $\sum_{i=1}^{N}\alpha_i y_i = 0$，得：

$$ \alpha_1 y_1 + \sum_{i=2}^{N} \alpha_i y_i = 0 $$

左右两边同乘一个 $y_1$，得：

$$ \alpha_1 {y_1}^2 + y_1 \sum_{i=2}^{N} \alpha_i y_i = 0 $$

因为 ${y_1}^2$ 恒为 1，显然：

$$ \alpha_1 = -y_1 \sum_{i=2}^{N} \alpha_i y_i $$

我们将 $\alpha_1$ 代入子问题，从而消去 $\alpha_1$。也就是说，对偶问题两个变量中只有一个是自由变量，实际上是单变量的优化问题，这样问题就更加简化了！

2. 两个变量的凸二次规划问题求解

通过变换，我们将子问题变成了只有 $\alpha_2$ 的单变量优化问题。如何求解 $\alpha_2$？考虑两种情形：

（1）考虑 $y_1 \times y_2$ 的两种不同情形

$$ y_1 = y_2 \Rightarrow \alpha_1 + \alpha_2 = k $$

$$ y_1 \neq y_2 \Rightarrow \alpha_1 - \alpha_2 = k $$

设 $L$ 与 $H$ 是在对角线段端点的上界和下界，由上图所示，要得到 $\alpha_2$ 的准确取值范围，上界我们取两个最大值的最小值，下界取两个最小值的最大值即可。由：

$$ L = \max(0, \alpha_1 + \alpha_2 - C), \quad H = \min(C, \alpha_1 + \alpha_2) $$

由：

$$ L = \max(0, \alpha_2 - \alpha_1), \quad H = \min(C, C + \alpha_2 - \alpha_1) $$

（2）不考虑约束条件求 $\alpha_{2}^{new,unc}$

首先，$\alpha_2$ 的约束条件很多，为了避免求解太繁，我们先不考虑上面两个条件的约束得到 $\alpha_{2}^{new,unc}$（unc，即 uncertain，不确定）的最优解，然后再求约束条件下的最优解 $\alpha_{2}^{new}$。

解：

设

$$ g(x) = \sum_{i=1}^{N} \alpha_i y_i K(x_i, x) + b $$

令误差

$$ E_i = g(x_i) - y_i = \left( \sum_{i=1}^{N} \alpha_j y_j K(x_i \cdot x_j) + b \right) - y_i, \quad i=1,2 $$

记

$$ v_i = \sum_{j=3}^{N} \alpha_j y_j K(x_i \cdot x_j) = g(x_i) - \sum_{j=1}^{N} \alpha_j y_j K(x_i \cdot x_j), \quad i=1,2 $$

故子问题的目标函数可以写为

$$ \begin{aligned} w(\alpha_1, \alpha_2) &= \frac{1}{2}K_{11}{\alpha_1}^2 + \frac{1}{2}K_{22}{\alpha_2}^2 + y_1 y_2 K_{12} \alpha_1 \alpha_2 \ & - (\alpha_1 + \alpha_2) + y_1 \alpha_1 v_1 + y_2 \alpha_2 v_2 \end{aligned} $$

因为

$$ \alpha_1 y_1 + \alpha_2 y_2 = k, \quad y_1^{2} = 1 $$

所以

$$ \alpha_1 = (k - \alpha_2 y_2) y_1 $$

代入目标函数，得：

$$ \begin{aligned} w(\alpha_2) &= \frac{1}{2}K_{11}{(k-\alpha_2 y_2)}^2 + \frac{1}{2}K_{22}{\alpha_2}^2 + y_2 K_{12}(k-\alpha_2 y_2)\alpha_2 \ & - (k - \alpha_2 y_2) y_1 - \alpha_2 + v_1(k - \alpha_2 y_2) + y_2 \alpha_2 v_2 \end{aligned} $$

这样目标函数只有一个未知参数了！针对单变量的凸二次规划问题，这太简单了。

（3）单变量的凸二次规划问题

对 $\alpha_2$ 求导并令其为零：

$$ \begin{aligned} \frac{\partial w}{\partial \alpha_2} &= -K_{11} k y_2 + K_{11} \alpha_2 + K_{22} \alpha_2 + y_2 K_{12} k - 2 y_2 K_{12} y_2 \alpha_2 + y_1 y_2 - 1 - v_1 y_2 + y_2 v_2 \ &= K_{11} \alpha_2 + K_{22} \alpha_2 + y_2 K_{12} k - 2 y_2 K_{12} \alpha_2 k - K_{11} k y_2 + y_1 y_2 - 1 - v_1 y_2 + y_2 v_2 = 0 \end{aligned} $$

得：

$$ \begin{aligned} (K_{11} + K_{22} - 2K_{12}) \alpha_2 &= y_2(y_2 - y_1 + k K_{11} - k K_{12} + v_1 - v_2) \ &= y_2 \left( y_2 - y_1 + k K_{11} - k K_{12} + \left( g(x_1) - \sum_{j=1}^{2}\alpha_j y_j K(x_1 \cdot x_j) - b \right) - \left( g(x_2) - \sum_{j=1}^{2}\alpha_j y_j K(x_2 \cdot x_j) - b \right) \right) \end{aligned} $$

将 $\alpha_1 y_1 + \alpha_2 y_2 = k$ 代入，得：

$$ \begin{aligned} (K_{11} + K_{22} - 2K_{12}) \alpha_{2}^{new,unc} &= y_2 ((y_2 - y_1 + g(x_1) - g(x_2) + (K_{11} + K_{22} - 2K_{12}) \alpha_{2}^{old} y_2)) \ &= (K_{11} + K_{22} - 2K_{12}) \alpha_2^{old} + y_2(E_1 - E_2) \end{aligned} $$

以下是详细的求解过程：

我们令 $\eta = K_{11} + K_{22} - 2K_{12}$，得：

$$ \alpha_{2}^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1 - E_2)}{\eta} $$

再考虑求解约束条件后的 $\alpha_{2}^{new}$

（4）考虑求解约束条件 $\alpha_{2}^{new}$

$$ \alpha_{2}^{new} = \begin{cases} H, & \alpha_{2}^{new,unc} \gt H \ \alpha_{2}^{new,unc}, & L \le \alpha_{2}^{new,unc} \le H \ L, & \alpha_{2}^{new,unc} \lt L \end{cases} $$

因为

$$ \alpha_{1}^{new} y_1 + \alpha_{2}^{new} y_2 = \alpha_{1}^{old} y_1 + \alpha_{2}^{old} y_2 $$

所以

$$ \alpha_{1}^{new} = \alpha_{1}^{old} + y_1 y_2 (\alpha_{2}^{old} - \alpha_{2}^{new}) $$

于是，我们经过上述的推导，终于就得到了对偶问题子问题的解 $(\alpha_{1}^{new}, \alpha_{2}^{new})$。

（5）重新计算 $b$ 和差值 $E_i$

在每次完成两个变量的优化后，我们还需要将 $\alpha_2^{new}$ 与 $\alpha_2^{old}$ 比较，如果变化的程度不大，则要重新计算阈值 $b$ 和差值 $E_i$。

3. 基于 Python 实现 SMO 的代码分析

这是基于 Python 实现 SVM 中的 SMO 算法，来自于《机器学习实战》，代码很容易读，基本可以与上文的公式推导完全对应，所以不太理解的地方，还是把 SMO 推导过程的来龙去脉先捋一捋吧！

from numpy import *
from time import sleep

# ==============================================================================
# 打开文件、两个辅助函数
# ==============================================================================
# 打开文件逐行读取数据，得到每行的类标签‘labelMat’和数据矩阵‘dataMat’
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():  # ‘fr.readlines()’逐行读取数据
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])  # 将每行数据的第一个和第二个位置储存到‘dataMat’矩阵
        labelMat.append(float(lineArr[2]))  # 每行的第三个是数据标签，存储到‘labelMat’矩阵
    return dataMat, labelMat

# 辅助函数 1：取两个不同下标的 alpha
def selectJrand(i, m):
    j = i  # we want to select any J not equal to i
    while (j == i):
        j = int(random.uniform(0, m))
    return j

# 辅助函数 2：用于调整大于 H 小于 L 的 alpha 值，对应 alpha2_new 的更新法则，alpha2_new 只能在 [L,H] 的区间范围之内
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

# ==============================================================================
# 简化版本 SMO 算法
# ==============================================================================
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):  # 5个参数：数据集、类别标签、常数c、容错率、退出前的最大循环次数
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()  # 类别标签‘classLabels’转置为列向量
    b = 0
    m, n = shape(dataMatrix)  # ‘shape’得到矩阵的行数m和列数n
    alphas = mat(zeros((m, 1)))  # 初始化alpha为元素全部为零的(m*1)列矩阵
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0  # 用于记录alpha是否已经进行优化
        for i in range(m):  # 外层循环
            fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            Ei = fXi - float(labelMat[i])  # 计算误差
            # 检查变量是否满足KKT条件，如果不满足，那么继续迭代，
            # 如果满足，那么最优化问题的解就得到了
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i, m)  # 内层循环
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b  # fXj为输入xj的预测值，对应本文公式(7)
                Ej = fXj - float(labelMat[j])  # 预测值与真实值之间的误差
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print("L==H")
                    continue  # 计算eta
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[j, :] * dataMatrix[j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue  # 求alpha2_new，对应alpha2_new的更新公式，注意eta与文中的符号刚好相反，所以这里是'-='
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                alphas[j] = clipAlpha(alphas[j], H, L)  # alpha2_new与alpha2_old比较，如果变化的程度不大，则要更新阈值b和误差值E
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    print("j not moving enough")
                    continue
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))  # 打印迭代次数、alpha优化的个数
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print("iteration number: %d" % iter)
    return b, alphas

七、贝叶斯

朴素贝叶斯法，即 Naive Bayesian Method，之所以 “naive”，大概是因为它只用到了浅显的概率论知识，（注意！本文没有任何的数学公式推导！）理解起来也相当容易。但不要看它 naive 就小瞧了它，朴素贝叶斯法基于贝叶斯定理和特征条件独立，是一种分类方法，它在分类任务中应用相当广泛。在这篇文章中，我会详细介绍贝叶斯法中的三个重要概念，以及用一个小故事和一个 Python 实现简单文本分类的例子帮助理解。

假设你的朋友近来发现笔记本玩游戏越来越卡，关键时候团战竟然掉帧卡顿，到手的五杀生生没了。为了更好地守护高地，他决定组装一台台式机，在网上苦苦搜寻，找来了一份主要部件的配置单，并征求你的建议，能不能胜任大型游戏：

内存 CPU 主板 硬盘
金士顿 骇客神条 8G Intel i5-6600 华硕 M5A78L-M 西数蓝盘 1TB

虽然你对计算机硬件不太懂，但是你会机器学习算法啊！这时，你手头正好有某神秘组织给你的计算机性能评测数据，那么如何利用好这些数据为你的朋友做出正确的选择呢？假设你有这方面的困惑，来，下面将向你展示如何用经典的贝叶斯方法解决这个问题。

贝叶斯其人

英国统计学家托马斯·贝叶斯（1701？-1761），后来成为了英国皇家学会成员，同时他还是一名哲学家。贝叶斯以前做过神父，为了证明上帝的存在，他建立了概率统计学原理，遗憾的是，这个愿望直到他死都没有实现。贝叶斯本人和他的研究工作在他当时并没有受到多少人的关注，他是如何入选英国皇家学会会员也鲜有记载，直到后来数学家拉普拉斯使他的工作重新为世人所肯定，贝叶斯方法才逐渐为世人瞩目。

托马斯·贝叶斯

三个简单的概念

朴素贝叶斯法的核心是贝叶斯定理，实际上是一个很简单的公式：

$$ P(Y|X)=\frac{P(Y)P(X|Y)}{P(X)} $$

假设我们有数据集 $Y=(y_1, y_2, \dots, y_m)$，$X=(x_1, x_2, \dots, x_n)$ 是数据集的分类标记，我们考虑几个基本的概念。

先验概率

先验概率分布是基于已有的数据集得出的，比如要判断一台计算机的性能（$Y=(strong, weak)$）如何，那么我们可以根据已有的评测数据来进行判断。由已有的评测数据，可以轻松得到计算机性能强弱的概率，这也就是所谓的先验概率。先验概率很容易计算：

$$

P(Y=y_i), \quad k=1, 2, \dots, m $$

条件概率

一般，要判断计算机性能强弱，我们会考虑一些什么特征 $X$ 呢？例如，处理器核心数多少、硬盘类型、显卡性能高低、内存大小等等。条件概率就是假设事件发生时，其他现象发生的概率，如考虑计算机性能很强情形下，处理器、硬盘、显卡指标分别所占的概率。

$$ P(X=x_j|Y=y_i), \quad k=1, 2, \dots, m $$

条件独立性假设

条件独立性是贝叶斯法中最重要的一个假设，也就是在分类 $y$ 在确定的情况下，各个条件之间是相互独立的，不然在计算公式就会有指数级的灾难。既然我们假定各个特征之间相互是不影响的，这样一来，计算就简化了许多。

$$ P(X=x_j|Y=y_i)=\prod_{j=1}^{n}P(x_j|Y=y_i) $$

了解了三个重要概念之后，贝叶斯方法的学习远远还没有结束，仅仅知道基本的概念不足以完成分类的任务。类似于 Logistic Regression，贝叶斯方法实际上也是一种基于概率的学习方法，它也是通过比较概率的相对大小来决定分类的结果。

后验概率最大化

在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。

计算 $P(Y=y_i|X=x_j)$ 是最终目标，即后验概率。最大化后验概率化也是贝叶斯方法的目标，也就是我们要让式的 $P(X|Y)$ 最大：

$$ \arg \max \prod_{j=1}^{n}P(x_j|Y=y_i) $$

贝叶斯估计

注意，朴素贝叶斯法和贝叶斯估计是不同的概念。朴素贝叶斯法中，用极大似然估计 可能会出现所要估计的概率值为 0 的情形，这种情形出现一般有两种原因：一是条件概率都很小，连乘会导致后验概率变得很小，一般会通过取对数的方式来避免；二是，当某个特征在训练集中没有与某个类同时出现过，那么直接计算的话，后验概率那就只能为零了，为了规避这种情况，通常要进行 “平滑”（Smoothing）处理，即拉普拉斯平滑（Laplace Smoothing），我们也称这一方法为贝叶斯估计。如下式：

$$ P(X=x_j|Y=y_i)=\frac{|I_{x_j}|+\lambda}{|I_{y_i=x_j}|+N_i\lambda} $$

式的 $\lambda$ 取 0 是就是极大似然估计。当 $\lambda$ 取 1 是，就是拉普拉斯平滑，它能够帮助避免训练样本集不充分而导致的概率估值为零的问题。

到底配置单是坑还是…？

为了解决你朋友的问题，你根据神秘组织给你的数据，这组数据根据内存容量、CPU、显卡等指标评估计算机性能。

内存容量 CPU 核心数 显卡 硬盘 性能强弱
8G 单核心 集成 机械 弱
8G 单核心 集成 固态 弱
4G 单核心 集成 机械 强
2G 双核心 集成 机械 强
2G 四核心 独立 机械 强
2G 四核心 独立 固态 弱
4G 四核心 独立 固态 强
8G 双核心 集成 机械 弱
8G 四核心 独立 机械 强
2G 双核心 独立 机械 强
8G 双核心 独立 固态 强
4G 双核心 集成 固态 强
4G 单核心 独立 机械 强
2G 双核心 集成 固态 弱

现在，贝叶斯就开始派上用场了！

首先，根据先验概率，性能强弱指标下只有强弱之分，令 $y_1$ 表示计算机性能 “强”，$y_2$ 表示计算机性能 “弱”。显然：

$$ \begin{aligned} P(Y=y_1) &= (9+1)/(14+2)=5/8 \ P(Y=y_0) &= (5+1)/(14+2)=3/8 \end{aligned} $$

由文章开头给出的配置单，对应的特征 $X=(8G, 4cores, integrated, hdd)$。然后，计算条件概率：

$$ \begin{aligned} P(\text{“8G”}|Y=y_1) &= (2+1)/(9+3)=3/12 \ P(\text{“8G”}|Y=y_0) &= (3+1)/(5+3)=4/8 \ P(\text{“4cores”}|Y=y_1) &= (3+1)/(9+3)=4/12 \ P(\text{“4cores”}|Y=y_0) &= (1+1)/(5+3)=2/8 \ P(\text{“integrated”}|Y=y_1) &= (3+1)/(9+2)=4/11 \ P(\text{“integrated”}|Y=y_0) &= (4+1)/(5+2)=5/7 \ P(\text{“hdd”}|Y=y_1) &= (3+1)/(9+2)=4/11 \ P(\text{“hdd”}|Y=y_0) &= (3+1)/(5+2)=4/7 \end{aligned} $$

对于给定的 $X=(\text{“8G”}, \text{“4cores”}, \text{“integrated”}, \text{“hdd”})$ 计算：

$$ P(Y=y_1)P(\text{“8G”}|Y=y_1)P(\text{“4cores”}|Y=y_1)P(\text{“integrated”}|Y=y_1)P(\text{“hdd”}|Y=y_1)=0.0069 $$

$$ P(Y=y_0)P(\text{“8G”}|Y=y_0)P(\text{“4cores”}|Y=y_0)P(\text{“integrated”}|Y=y_0)P(\text{“hdd”}|Y=y_0)=0.0191 $$

因为 $P(Y=y_0)P(\text{“8G”}|Y=y_0)P(\text{“4cores”}|Y=y_0)P(\text{“integrated”}|Y=y_0)P(\text{“hdd”}|Y=y_0)$ 较大，所以 $Y=y_0$，从而可以初步判断按照此配置单组装的电脑性能为弱，绝对又是一个坑！（团战掉线，就跟那些无止尽刷野的坑货一样，都应该封号！）

说点题外话，上面例子中提到的配置单问题应该出现在了显卡上，集成显卡的属性使得整个性能大打折扣，所以关键的地方还是要抛弃原有的主板，考虑买一块独立显卡。

例子：利用贝叶斯进行简单的文本分类

本例所用到的代码来自《机器学习实战》，非常值得推荐。代码虽然不多，但是给我最大的体会就是，懂算法的原理和实实在在在工程中应用实现是完全不同的两回事。正如本博客翻译的 Numpy 入门教程之前，我一直不明白在图像上怎么进行机器学习的工程应用，后来我翻译完教材之后才恍然大悟，原来图片的每一个像素点可以视为一个数字，所有的像素点不就组成了一个数组吗？开始看贝叶斯的时候，我也一直纳闷，这个贝叶斯方法怎么就可以用于文本分类呢？看不懂的时候，我就联想本文讲的这个组装电脑的故事，一点一点理解，明白了我得先有一个 数据集，然后，在现有数据集的基础上计算先验概率，计算先验概率的时候还得注意数值下溢的问题，不然无法理解代码中的 log(1.0 - pClass1) 和 log(pClass1)。光看算法，光看书没用啊！拿个例子来做一做，理解会更加深刻！

处理过程

  1. 由样本数据集创建词汇表
  2. 根据输入的待划分数据创建词向量
  3. 计算先验概率，然后比较后验概率
  4. 测试
from numpy import *

# 导入样本数据集
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 1 is abusive, 0 not
    return postingList, classVec

# 由数据集创建词汇表
def createVocabList(dataSet):
    vocabSet = set([])  # 创建一个空集，集合内的元素各不相同
    for document in dataSet:
        vocabSet = vocabSet | set(document)  # union of the two sets
    return list(vocabSet)

# 由输入词汇创建词向量
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1  # 如果 word 在词汇表中，则向量相应位置为 1
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # 实验样本中正例的个数，根据第一个函数，pAbusive=0.5
    p0Num = ones(numWords)
    p1Num = ones(numWords)  # change to ones()
    p0Denom = 2.0
    p1Denom = 2.0  # 所有词的个数出现次数初始化为 1，为了避免概率出现 0 的情形
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:  # 一旦某个词在文档中出现，则该词对应的个数就要加 1
            p1Num += trainMatrix[i]  # trainMatrix 是一个 array，故 trainMatrix[i] 是 '[]'
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num / p1Denom)
    p0Vect = log(p0Num / p0Denom)
    return p0Vect, p1Vect, pAbusive

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)  # element-wise mult
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

def testingNB():
    listOPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses))
    
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
    
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))

个人在理解 trainNB0(trainMatrix, trainCategory) 这个函数的时候卡住了一下，因为我事先没注意到 trainMatrix 是一个 array，因为它的数据类型是列表，所以我不明白为什么 p1Num 和 trainMatrix[i] 可以直接叠加（一个数组跟一个数字相加干嘛呢？）。另外，trainNB0(trainMatrix, trainCategory) 还用到了拉普拉斯平滑的手段来防止概率为 0 的情形。这个例子还是存在不足之处的，比如说，数据集太小导致泛化能力不佳，如果我用一个在样本数据集中从未出现过的词来做测试，这个时候测试函数就无法正确检测了。

参考

  1. 后验概率 - 维基百科
  2. 《统计学习方法》 李航
  3. 《机器学习》 周志华
  4. 《机器学习实战》
  5. 一些关于贝叶斯的文章
    1. 学界 | 清华大学计算机系朱军教授：机器学习里的贝叶斯基本理论、模型和算法
    2. 贝叶斯推断及其互联网应用（一）：定理简介
    3. 数学之美番外篇：平凡而又神奇的贝叶斯方法

八、神经网络

机器学习中的神经网络（Neural Networks）算法受到生物界神经系统处理信息的启发，比如大脑处理信息的方式。跟人类一样，神经网络的训练也是一个学习的过程，通过大量的学习，神经网络能够完成特定的任务，比如图像分类识别、疾病预测判断等等。在这篇文章里将简单介绍神经元工作原理和神经网络模型，重点在于理解反向传导算法（BP）中参数的更新过程，并用一个实例解释了 BP 算法。

本文目录

神经网络

理解神经元的工作原理

“神经网络” 一词起源于早先模拟（mimic）人类大脑的研究中，而发展到今天的 “神经网络” 早就已经是一个庞大的交叉学科领域，当然本文讨论的范围在机器学习与神经网络交叉的部分。在进行正式讨论之前，我们有必要先了解一些神经网络的前世今生。

关于神经网络最广泛的定义是：

神经网络是由具有适应性的简单单元组成的广泛并且并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应（Kohonen，1988）

从生物学的角度，大脑是人体的最高指挥中心，人的听觉、嗅觉、味觉、触觉、视觉等等感官感受都是通过神经网络来接收、传递、处理的。

神经网络的基本单元是神经元（neuron），神经元的基本组成有细胞核（cell）、树突（dendrite）、轴突（axon）、轴突末梢（axon terminal）。神经元有接收、处理、传递信息的功能。

典型的神经元结构1

当树突从其他神经元接收化学物质（多巴胺、乙酰胆碱），神经元会变得 “兴奋”，于是通过轴突将信息传递给另外的神经元，化学物质在树突与轴突的传递形成电流，如果两个神经元之间的电位差别超过 “阈值”，那么它便会被 “激活”，这就是神经元的基本工作模式。

在人类的大脑中约有 860 亿计个神经元，$10^{14}$ 到 $10^{15}$ 个突触（synapse），正是这些简单的神经元组合可以完成各类复杂工作，于是成就了地球上最智慧的生物 —— 人类。

简单神经元模型

回到机器学习，首先，我们从最简单的神经元模型讲起，也就是神经网络中仅仅只有一个神经元（Single Neuron）的情形，如图示：

一个简单的神经元模型

在上面这个模型中，神经元收到来自其他来自 3 个神经元（$x_i, i=1, \dots, 3$）的信息，即输入（Input），这些输入通过带权重（Weights）（$w_j, j=0, 1, \dots, 3$）的连接进行传递，对线性组合（$w \cdot x$）的传递汇总，进行激活（Activation）处理之后再与当前神经元的阈值进行比较，如果大于阈值，那么该神经元则被激活。注意，这里我们通常将 $x_0$ 和 $w_0$ 均取为 1，即把 $w_0$ 当做偏置项（Bias）。

将上述过程与生物学的神经元类比，蓝色的圈表示突触，桔色的圈表示细胞核，蓝色与桔色的圈之间的连接表示树突，激活之后的计算结果就好比电位差，只有存在电位差，神经元才有可能会被激活。

典型的神经元结构2

我们通常选择 Sigmoid 函数作为激活函数 $f(\cdot)$（Activation Function）：

$$f(w,x)=\frac{1}{1+e^{-w^Tx}}$$

细心的读者可能会有疑惑，前面说好的 “阈值比较” 过程去哪里了？不是还有一个判断的过程吗？其实，神经元模型中的激活函数便完成了这个任务，观察 Sigmoid 函数：

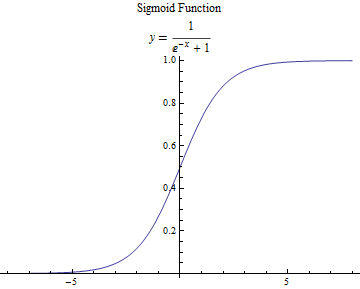
Sigmoid函数

可以看出，线性组合经过 Sigmoid 函数处理，输出值被映射到 $(0, 1)$ 的范围内，所以我们可以在此范围灵活地设置阈值以决定神经元是否被激活。“1” 对应于激活，“0” 对应于抑制。把许多个这样的神经元模型按照一定的结构联系起来，就得到了神经网络。除了 Sigmoid 函数可以作为激活函数，常用的激活函数还有双曲正切函数（tanh）、ReLU（Rectified Linear Unit）、Maxout 等，这里就不详细展开。

神经网络模型

像这样只有输入层和输出层两层的神经元模型也被叫做感知机，感知机能够实现简单的与、或、非逻辑运算，除此之外，感知机学习能力非常有限，对于线性不可分的问题束手无策。

讲到这里，有必要插播一段神经网络研究的历史，神经网络的发展可谓一波三折：

首次尝试：1943 年 McCulloch 和 Pitts 基于神经学奠定了神经网络的基础，拥有单个神经元的神经网络又被称为是 “M-P 神经元模型”，M-P 神经元模型能够解决简单的逻辑问题。除此之外，还有两队人马也加入到了神经网络的研究队伍，分别是 IBM 和 (Farley and Clark, 1954; Rochester, Holland, Haibit and Duda, 1956) 等人。

百家争鸣：神经网络在多个领域发扬光大，如心理学、工程行业。1958 年 Rosenblatt 设计并发展了感知机，使它能够进行简单图像识别，在当时引起了极大轰动。

十年停顿：1969 年 Minsky 和 Papert 写了一本名为《感知机》的书，书中详细论证了单层感知机无法解决非线性问题，而多层神经网络的训练算法则看不到希望，这一悲观情绪直接导致了神经网络研究的十年停顿，研究经费大幅缩减。

“…our intuitive judgment that the extension (to multilayer systems) is sterile”

“··· 我们最先对多层神经网络系统的判断是徒劳的”

第二春：1986 年 Rumelhar 和 Hinton 等人提出了反向传播（Backpropagation，BP）算法，解决了两层神经网络所需要的复杂计算量问题，从而带动了业界使用两层神经网络研究的热潮。

再陷低谷：20 世纪 90 年代中期，Vapnik 提出了支持向量机方法，由于不需要调参、全局最优、高效，并在比赛中表现非常好，支持向量机的出现打败神经网络，神经网络再陷低谷。

横空出世：2006 年 Hinton 在《科学》发表论文，提出 “深度学习” 的概念。2012 年，Hinton 和他的两个学生在 ImageNet 图像分类比赛中借助深度学习一举夺魁，深度学习横空出世，谁与争锋！

Hinton

多层神经网络

多层神经网络

神经网络最左边的一层叫做输入层（Input Layer），最右边的叫做输出层（Output Layer），中间的所有节点则称为隐藏层（Hidden Layer）。一般神经网络越复杂，它的隐藏层数则越多，理论上能够胜任的任务也就越复杂。上面的神经网络中，一共有三个输入单元（最下方的偏置项不算），三个隐藏单元和一个输出单元，它是一个回归模型（Regression Model）。

为了更好地描述神经网络，我们引入三个参数，系数 $W_{ij}^{(l)}$ 表示第 $l$ 层的 $j$ 个单元与第 $(l+1)$ 层第 $i$ 单元的权重，系数 $b_i^{(l)}$ 表示第 $l$ 层第 $i$ 单元的偏置项（注意，偏置项的权重取 1），$a_i^{(l)}$ 表示 $l$ 层第 $i$ 个单元的激活值。

当神经网络得到输入 $x_n$，$n$ 个输入由带权重的连接分别传递到下一层的各个节点，下一层节点将上一层传递下来的数值汇总传入激活函数 $f(\cdot)$，神经网络的参数计算过程如下：

$$ \begin{aligned} a_1^{(2)} &= f(W_{11}^{(1)}x_1+W_{12}^{(1)}x_2+W_{13}^{(1)}x_3+b_1^{(1)}) \ a_2^{(2)} &= f(W_{21}^{(1)}x_1+W_{22}^{(1)}x_2+W_{23}^{(1)}x_3+b_2^{(1)}) \ a_3^{(2)} &= f(W_{31}^{(1)}x_1+W_{32}^{(1)}x_2+W_{33}^{(1)}x_3+b_3^{(1)}) \ h(W,x) &= a_1^{3}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+W_{13}^{(2)}a_3^{(2)}+b_1^{(2)}) \end{aligned} $$

（注：系数 $W_{ij}^{(l)}$ 表示第 $l$ 层的 $j$ 个单元与第 $(l+1)$ 层第 $i$ 单元的权重）

我们可以简洁一点表示，令：

$$ \begin{aligned} z^{(l+1)} &= W^{(l)}x + b^{(l)} \ a^{(l+1)} &= f(z^{(l+1)}) \end{aligned} $$

不考虑偏置项，拥有三个输入单元，三个隐藏单元和一个输出单元的神经网络涉及到 12（3×3+3×1）个参数。

考虑该神经网络数值计算过程，像这样给定输入和参数，数值计算一层一层往前推进然后得到一个输出，没有反馈，没有循环的神经网络，我们也给它取了一个名字，前馈神经网络（Feedforward Neural Network）。

实际上，神经网络模型还可以有多个隐藏层，每个隐藏层又可以设定多个参数；神经网络的输出也可以多个，如果具有多个输出，那么神经网络模型任务就由回归（一个输出）变成分类（多个输出）了。理论上神经网络越复杂，参数越多，它能够完成的任务就更复杂。比如 2015 年微软亚洲研究院在 ImageNet 计算机识别挑战赛中使用了深达百层的神经网络，比以往成功的神经网络层数多了 5 倍以上，系统错误率低至 3.57%。

反向传导（BP）算法思路

反向传导算法（Backpropagation Algorithm，简称 BP 算法）是优化神经网络参数迭代的主要算法，BP 算法的思路是：

  1. 前馈传导运算，得到各输出层的输出；
  2. 从输出层反推进行反向传导计算，利用梯度下降算法更新参数

在进行反向传导算法推导之前，我们有必要了解几个重要的概念，比如定义损失函数，在参数初始化上要保证随机性，以及最重要的是理解残差的概念。

神经网络的参数众多，而优化神经网络参数用到的批量梯度下降算法中主要的计算又是众多的求偏导计算，所以在进行反向求导时一定要明白参数之间的联系。

定义损失函数

进行优化之前，要定义优化的目标是谁，即目标函数。对于单个样本，定义损失函数为：

$$J(W,b;x,y)=\frac{1}{2} {||h(W,b,x)-y||}^2$$

那么对于整个样本集，损失函数可以定义为：

$$J(W,b)= \frac{1}{m} \sum J(W,b;x,y) + \frac{\lambda}{2} \sum W^2$$

上式中的第一项为平方差项，第二项为正则化项，目的是为了防止过拟合。我们的目标是针对参数 $W$ 和 $b$ 来求 $J(W,b)$ 的最小值。

随机初始化参数

为了求解神经网络，我们需要将参数初始化为一个很小的，接近零的随机数，然后对目标函数使用优化算法。注意，如果所有的参数都是相同的，那么所有的隐藏单元都会得到相同的值，如此一来便失去了优化的意义，随机初始化就是要消除它。通常，我们可以让随机参数服从一个很小的正态分布。

计算残差

残差在反向传导算法中是一个非常非常非常重要，而且有点点难理解的概念！！！

本文中残差的定义来自斯坦福的教程，原教程的公式推导我觉得有点太 “详细” 了，经常是看到公式后面忘了字母的定义是什么，所以我在此基础上做了简化，希望能够方便理解。

在这之前，务必记住以下两个重要定义：

$$ z^{(l+1)} = W^{(l)}x + b^{(l)} $$

我们定义残差为：

$$ \delta_i^{(nl)} = \frac {\partial} {\partial{z_i^{(nl)}}} \frac{1}{2} (y_i - a_j^{(nl)})^2 \ =\frac {\partial} {\partial{z_i^{(nl)}}} \frac{1}{2} (y_i - f(z_j^{(nl)}))^2 \ =-(y_i-f(z_i^{(nl)}))\cdot f’(z_i^{(nl)})\ =-(y_i-a_i^{(nl)}) \cdot f’(z_i^{(nl)})\ $$

需要注意的是，残差中求偏导的对象是 $z_i^{(nl)}$，至于为什么是 $z_i^{(nl)}$ 而不是权重系数，下面会具体说明。

为什么是 $z_i^{(nl)}$?

式给出了 $nl$ 层，也就是输出层向隐藏层的残差，那么考虑一个只有一个隐藏层的神经网络，再考虑向输入层推进呢？也就是求解 $\delta_i^{(nl-1)}$，有：

$$ \delta_i^{(nl-1)} = \frac {\partial} {\partial{z_i^{(nl-1)}}} \frac{1}{2} \sum (y_i - a_j^{(nl)})^2 \ =\sum \frac {\partial} {\partial{z_i^{(nl-1)}}} \frac{1}{2} (y_i - f(z_j^{(nl)}))^2 \ =\sum -(y_i-f(z_i^{(nl)}))\cdot f’(z_j^{(nl)}) \cdot \frac{\partial z_j^{(nl)}}{\partial z_j^{(nl-1)}}\ =\sum \delta_j^{(nl)} \frac{\partial z_j^{(nl)}} {\partial z_j^{(nl-1)}}\ =(\sum \delta_j^{(nl)} W^{nl-1})f’(z_i^{(nl-1)})\ $$

这下就终于明白了为什么残差中求偏导的对象是 $z_i^{(nl)}$ 了，因为 $z_i^{(nl)}=W^{(nl)}x+b$，神经网络中各个层的权重参数众多，所以这样一来只需要对 $z_i^{(nl)}$ 再求一次偏导，便可以得到想要的权重系数的偏导数。

BP 算法的一次实例更新迭代

第一步：前馈传导

如下图，考虑一个神经网络，该神经网络一共有三层，其中有一个隐藏层，两个输入单元，两个隐藏层单元，两个输出单元，外加两个取值为 1 的偏置项。

以隐藏层第一个激活值 $a_1^{(2)}$ 计算为例（神经网络选择 Sigmoid 函数作为激活函数），连接线上的数字为随机初始化的权重参数，输入节点经加权汇总之后汇入隐藏层。计算方法如下：

$$a_1^{(3)}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+b_1^{(2)})$$

$$a_2^{(3)}=f(W_{21}^{(2)}a_1^{(2)}+W_{22}^{(2)}a_2^{(2)}+b_1^{(2)})$$

前馈传导

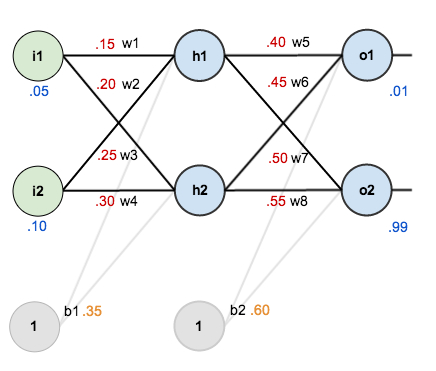
经过前馈传导运算，神经网络最终得到两个输出，分别是 0.7513 和 0.7729。假设真实标签为 [0.01, 0.99]，输出和真实标签有误差，需要对其进行优化。

第二步：反向传导

计算总误差，总的误差：

$$ E_T = \frac{1}{2}\sum (y_i - a^{(nl)})^2, \quad a^{(nl)} \text{表示输出层} $$

所以：

$$ E_T = \frac{1}{2}(0.01-0.7513)^2+\frac{1}{2}(0.99-0.7729)^2 = 0.298$$

输出层 → 隐藏层的权值更新 $W_{11}^{(2)}$

考虑 $W_{11}^{(2)}$ 对整体误差的影响，是一个链式求导的过程。

有：

$$\frac {\partial{E_T}} {\partial{z_{11}^{(3)}}} =\frac {\partial{E_T}} {\partial{a_1^{(3)}}} \frac{\partial{a_1^{(3)}}}{\partial{z_{11}^{(3)}}}$$

其中：

$ z_{11}^{(3)} = f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+b_1^{(2)}) $

由式，以及 Sigmoid 函数的求导法则，可得：

$$\delta_1^{3}=-(0.01-0.7513)0.7513(1-0.7513)=0.1385$$

因为需要更新的权值是 $W_{11}^{(2)}$，所以再对 $z_{11}^{(3)}$ 求 $W_{11}^{(2)}$ 偏导即可。假定学习率为 0.5，那么 $W_{11}^{(2)}$ 更新如下：

$$ W_{11}^{(2)} := W_{11}^{(2)} - \eta \cdot \delta_1^{3} \cdot a_1^{(2)} $$

即：

$$ W_{11}^{(2)} := 0.4 -0.50.13850.5932=0.3589 $$

同理，我们也可以求得 $\delta_2^{3}$，并更新相应的权值 $W_{2j}^{(2)}$，计算过程可以参照 $W_{11}^{(2)}$ 的更新：

$$ \delta_2^{3}= -(0.99-0.7729)0.7529(1-0.7529)=-0.0381$$

隐藏层 → 输入层权值更新 $ W_{11}^{(1)} $

然而仅仅更新一层的参数是不够的，既然是反向传导，参数的更新便是从右至左的过程，如果要更新输入层至隐藏层之间的参数，又该如何计算呢？如下图，$W_{11}^{1}$ 的权值（0.15）影响到了两个输出：

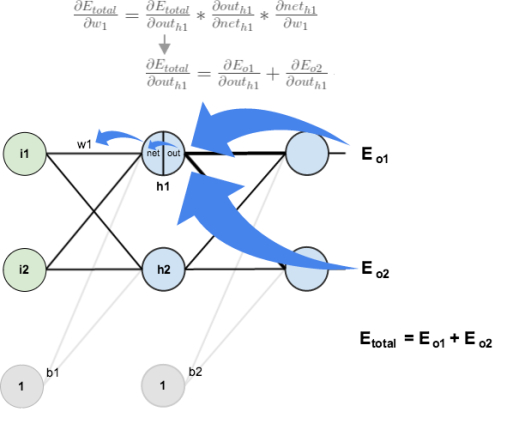
$W_{11}^{(1)}$ 影响到 $a_1^{(2)}$ 的输出，而 $a_1^{(2)}$ 接受来自两个输出 $a_1^{(3)}$ 和 $a_2^{(3)}$ 的误差，所以我们先将偏导数进行到 $a_1^{(2)}$，实际上是求解 $\sum \delta_j^{(3)} W_{ij}^{2}$：

$$ \begin{aligned} \sum \delta_j^{(3)} W_{ij}^{(2)} &= \frac {\partial{E_T}} {\partial{a_1^{(3)}}} \frac{\partial{a_1^{(3)}}}{\partial {a_1^{(2)}}} + \frac {\partial{E_T}} {\partial{a_2^{(3)}}} \frac{\partial{a_2^{(3)}}}{\partial {a_1^{(2)}}} \ &=0.1385*0.4+(-0.0381)*0.5 \ &=0.0538+(-0.0190)\&=0.0348 \ \end{aligned} $$

至此，来自两个输出的权值影响就全部汇集到了 $a_1^{(2)}$。接下来，我们只需要考虑 $W_{11}^{(1)}$ 对 $a_1^{(2)}$ 的影响了，这就变得简单多啦！由式可得：

$$ f’(z_1^{2}) = 0.5932*(1-0.5932) = 0.2413 $$

$$ \delta_1^{(2)} = (\sum \delta_j^{(3)} W_{ij}^{(2)}) \cdot f’(z_1^{2}) $$

故 $ W_{11}^{(1)} $ 权值更新如下：

$$ W_{11}^{(1)} := W_{11}^{(1)} - \eta \cdot \delta_1^{(2)} \cdot a_1^{(1)} = 0.1498 $$ $$ W_{11}^{(1)} := 0.15 - 0.5 * 0.0348 * 0.2413 * 0.05 = 0.1498 $$

反向传导最关键的地方在于残差的数值传递，即式，一定要正确理解 $\delta_1^{(2)}$ 与 $\delta_j^{(3)}$ 之间是如何联系起来的！神经网络中的其他参数也可以按照同样的方法进行更新，本文不再赘述。

本文中给出的例子有两个输出，故数值传递比只有一个输出的要更复杂，如果只有一个输出的话，那我们计算 $\frac {\partial{E_T}} {\partial {a_1^{(2)}}}$ 就不用考虑 $a_2^{(3)}$ 的影响

其实这样理解起来挺麻烦的，我们换一个角度看看：

$$\frac {\partial {a_1^{(2)}}}{\partial W_{11}^{(1)}}=0.5932*(1-0.5932)*0.05=0.0120$$

$$ \frac {\partial{E_T}}{\partial W_{11}^{(1)}} = 0.0348*0.0120=0.0004 $$

再应用梯度下降算法，$ W_{11}^{(1)} $ 权值更新如下：

$$ W_{11}^{(1)} := 0.15 - 0.5 * 0.0004 = 0.1498 $$

跟上面的方法得出的结果也是一样的，这里并不是说从残差的角度去计算就不好，而是从一个平时我们习惯的视角去更新参数能够加深理解。

参考文献

  1. 反向传播算法 Python 代码 | 我爱自然语言处理
  2. 神经网络 - Ufldl
  3. 神經元 - 维基百科
  4. 微软实现深层神经网络重大技术突破 - 微软亚洲研究院
  5. CS231n Convolutional Neural Networks for Visual Recognition
  6. Neural Networks
  7. 《机器学习》 周志华
  8. 《统计学习方法》 李航
  9. 《The Elements of Statistical Learning》Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
  10. A Step by Step Backpropagation Example – Matt Mazur

九、主成分分析 PCA

主成分分析（Principal Components Analysis，PCA）是一种无监督降维技术，它广泛应用于电视信号传输、图像压缩等领域。当面临的数据维数很高的时候，我们很难发现隐藏在数据中的模式和有用的信息，并且给建模带来不便，PCA 是一种常见的解决这类问题的手段。PCA 的目的在于寻找一个能够对所有样本进行恰当表达的超平面，这个超平面具有两个性质：最近重构性（样本点到这个超平面的距离都足够近）和最大可分性（样本点在这个超平面上的投影能够尽可能分开）。

以上说的可能有点抽象，举个例子，比如晚上你在路灯下行走，当你走到路灯的正底下或者仅仅偏离正底下一点点，光凭一丁点阴影是没有办法判断你的性别的。当你继续往前走，灯光把影子越拉越长，阴影中包含的信息逐渐多了起来，比如胖瘦、头发、衣着等等，此时判断性别就相对简单多了。我举这个例子的用意在于，如果找到一个好的投射坐标系（这是关键！），就能用最小的成本保留原始数据最多的信息。

1. 主成分分析原理

在 PCA 中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。

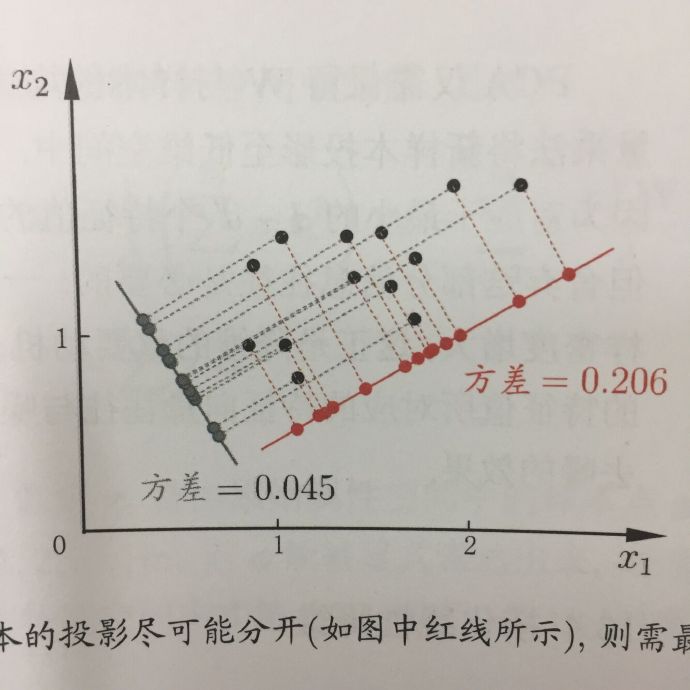
为什么要找原始数据中方差最大的方向？在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如下图，数据投射到红色向量（方差为 0.206）上显然能够更好地将数据隔开，并且能够保留原数据集的最大信息。

图片来源：《机器学习》周志华

PCA 的优化目标是什么？假设对数据已经进行了去均值处理 $\sum{x_i}=0$，且新坐标系为 $W$，并且将维度降低，得到低维坐标中的投影 $W^Tx$。因为我们需要尽可能地将样本点分开，所以需要寻找方差最大的方向 $W$，由此 PCA 的优化目标：

$$ \begin{aligned} \max \quad & tr(W^TXX^TW) \ s.t. \quad & W^TW=I \end{aligned} $$

然后对上式采用拉格朗日乘子法，

$$ XX^TW=\lambda W $$

是不是很熟悉？这不就是对协方差矩阵 $XX^T$ 求特征值和特征向量嘛！$W$ 可能包含多个向量，主成分的个数对应着取 $W$ 中多少个特征向量，需要留下多少的信息取决于自身的决定。

2. 预备数学知识

在接触到 PCA 之前，大学学过的线性代数和概率统计的知识有点忘了，在学习的时候顺带把相关的知识复习一下。

2.1 协方差

协方差在概率统计中用于衡量两个变量之间的总体误差，方差是协方差的一种特殊情况。

$$ \begin{aligned} cov(X,Y) &= \frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{n-1} \ var(X) &= \frac{\sum_{i=1}^{n}(X_i-\bar{X})(X_i-\bar{X})}{n-1} \end{aligned} $$

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。

如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

如果两个变量相互独立，那么它们之间的协方差就是零。

上面讨论的情形均是针对两个变量，如果有多个变量的存在呢？比如有 $x, y, z$ 三个变量，那么便需要计算三对协方差，为了方便，我们将协方差放进一个矩阵，称为协方差矩阵（covariance matrix）。

2.2 特征值和特征向量

关于特征值和特征向量的基础知识可参照线性代数第五版（高等教育出版社）“方阵的特征值和特征向量” p117。

3. PCA 基本步骤

了解了一些基本的数学知识之后，便可以开始着手 PCA 的工作了。

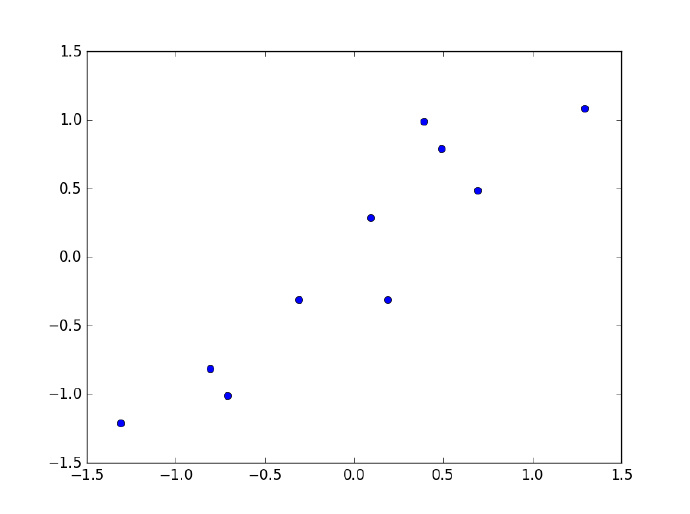
假设我们需要对如下数据做降维处理，需求是将其从 2 维降到 1 维，该如何处理呢？

$$ \begin{array}{c|lcr} Data & \text{} & \text{} \ \hline x & 2.5 & 0.5 & 2.2 & 1.9 & 3.1 & 2.3 & 2 & 1 & 1.5 & 1.1 \ y & 2.4 & 0.7 & 2.9 & 2.2 & 3.0 & 2.7 & 1.6 & 1.1 & 1.6 & 0.9 \ \end{array} $$

PCA 主要有以下几个步骤：

  1. 去除平均值，做中心化处理

$$ \begin{array}{c|lcr} Data\ Adjust & \text{} & \text{} \ \hline x & .695 & -1.31 & .39 & .09 & 1.29 & .49 & .19 & -.81 & -.31 & -.71 \ y & .49 & -1.21 & .99 & .29 & 1.09 & .79 & -.31 & -.81 & -.31 & -1.01 \ \end{array} $$

  1. 计算协方差矩阵

  1. 计算协方差矩阵的特征值（eigenvalue）和特征向量（eigenvector）

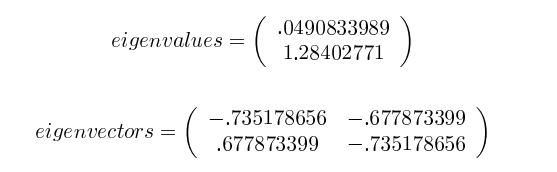
  1. 将特征值从大到小排列，选择前 $k$ 个特征值和其相对应的特征向量，并组成新的特征向量矩阵。在本例中只有两个特征值，所以 $k=1$，选择 $1.28402771$ 和相应的特征向量（Feature vector）$(-0.677873399, -0.735178656)^T$。

  2. 将数据集映射到新空间，生成新的数据集。调整后的数据集是 $10 \times 2$ 的矩阵，与特征向量（$n \times k$）相乘之后，原始数据集由 $n=2$ 维变成 $k=1$ 维。

$$ New\ data = Data\ Adjust \times Feature\ vector $$

降维后的数据集

降维给数据带来了两个影响：

4. 基于 Python 实现 PCA

将上面的例子用 Python 来实现一遍：

import numpy as np
import matplotlib.pyplot as plt

# 导入数据，转换为矩阵
x = np.array([2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1])
y = np.array([2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9])

# 去除平均值
remove_mean_x = x - np.mean(x)
remove_mean_y = y - np.mean(y)
data = np.matrix([[remove_mean_x[i], remove_mean_y[i]] for i in range(len(remove_mean_x))])

plt.plot(remove_mean_x, remove_mean_y, 'o')
plt.show()

去除平均值后的数据 

# 计算协方差矩阵
cov = np.cov(remove_mean_x, remove_mean_y)
# 计算特征值和特征向量
eig_value, eig_vector = np.linalg.eig(cov)

计算得到的协方差和特征向量矩阵，协方差矩阵是对称阵，故得到的特征向量之间是相互正交的。

# 协方差矩阵
[[ 0.61655556  0.61544444]
 [ 0.61544444  0.71655556]]
# 特征值
[ 0.0490834   1.28402771]
# 特征向量
[[-0.73517866 -0.6778734 ]
 [ 0.6778734  -0.73517866]]

# 选择特征向量
eig_pairs = [(np.abs(eig_value[i]), eig_vector[:, i]) for i in range(len(eig_value))]
eig_pairs.sort(reverse=True)
feature = eig_pairs[0][1]

# 将数据映射到新空间，得到降维后的数据
rot_data = (np.dot(eig_vector, np.transpose(data))).T
new_data = (np.dot(feature, np.transpose(data))).T

# 降维后的数据
[[-0.82797019]
 [ 1.77758033]
 [-0.99219749]
 [-0.27421042]
 [-1.67580142]
 [-0.9129491 ]
 [ 0.09910944]
 [ 1.14457216]
 [ 0.43804614]
 [ 1.22382056]]

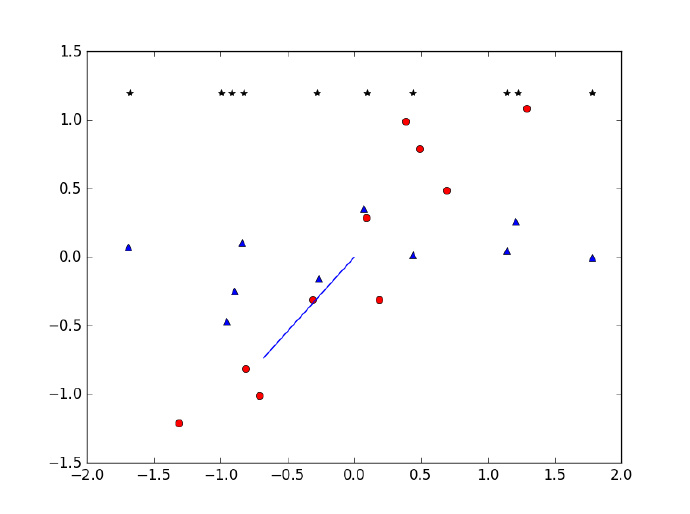
蓝色线条为选择的特征向量，红点为移除平均值之后的数据集，星点为降维后得到的数据。

# 降维前后数据集的对比
plt.plot(remove_mean_x, remove_mean_y, 'o', color='red')
plt.plot([eig_vector[:, 1][0], 0], [eig_vector[:, 1][1], 0], color='blue')
plt.plot([eig_vector[:, 0][0], 0], [eig_vector[:, 0][1], 0], color='blue')
plt.plot(rot_data[:, 0], rot_data[:, 1], '^', color='blue')
plt.plot(new_data[:, 0], [1.2] * 10, '*', color='black')
plt.show()

原数据集和降维后的数据集

推荐阅读

  1. A tutorial on Principal Components Analysis
  2. Principal Component Analysis Explained Visually

十、k 均值

在用户增长分析过程中有时除了需要预测用户的行为，还需要把用户细分为差异比较大的群体，然后针对不同的群体采取相应的运营手段，即用户分群。在机器学习的算法中有一个专门的领域——聚类算法，聚类是一种了解数据内在结构的方法，它通过将数据集中的样本划分为若干不相交的子集，每个子集称为一个“簇”（cluster）。如何定义簇以及簇的数量则完全人工自行决定。在先前的文章中涉及到的算法都是监督学习，现在我们开始接触到机器学习中第一个无监督学习算法——k-均值。不同于以往的数据集，无监督学习所用到的数据集都是没有标签的，也就是事先并不知道数据的内在性质及规律。

k-均值的最终目的是最小化平方误差：

$$ E = \sum_{i=1}^{k}\sum_{x\in C_i}{||x-\mu_i||}_2^2 $$

一、k-means 基本思路

k-均值算法的基本思路：

  1. 随机生成 k 个随机质心
  2. 计算样本值到质心之间的欧式距离，将样本点划分到距离最近的质心
  3. 重新更新各个簇的质心位置
  4. 重复 2-3 步，直到质心位置不再变化
  5. 得出输出结果

二、基于 Python 的 k 均值算法实现

from numpy import *

# 导入文件
file_name = "E:/Python/mla/Ch10/testSet.txt"

def load_data(file_name):
    data_mat = []
    fr = open(file_name)
    for line in fr.readlines():
        # 将文本文档的每一行转换成浮点型并添加到矩阵中
        current_line = line.strip().split('\t')
        data_mat.append([float(current_line[0]), float(current_line[1])])
        dataset = mat(data_mat)
    return dataset

dataset = load_data(file_name)

# 计算向量间欧几里得距离
def cal_dist(vec_a, vec_b):
    return sqrt(sum(power(vec_a - vec_b, 2)))

# 生成k个随机质心（centroids）
def rand_centroid(dataset, k):
    n = shape(dataset)[1]
    centroids = mat(zeros((k, n)))
    for j in range(n):
        min_j = min(dataset[:, j])
        range_j = float(max(dataset[:, j]) - min_j)
        centroids[:, j] = min_j + range_j * random.rand(k, 1)
    return centroids

# k均值聚类算法
def k_means(dataset, k):
    m = shape(dataset)[0] # 获取数据的行数m
    # 簇分配结果矩阵'cluster'包含两列：
    # 第一列记录簇索引值，第二列存储误差
    cluster = mat(zeros((m, 2)))
    centroids = rand_centroid(dataset, k)
    # 创建一个标志变量'cluster_changed'
    cluster_changed = True
    while cluster_changed:
        cluster_changed = False
        for i in range(m):
            min_dist = inf
            min_index = -1
            # 分别计算'dataset'中第i个点与k个质心之间的欧几里得距离，
            # 并将距离最小的质心的索引赋给簇分配结果
            for j in range(k):
                dist_i_j = cal_dist(centroids[j, :], dataset[i, :])
                if dist_i_j < min_dist:
                    min_dist = dist_i_j
                    min_index = j
            if cluster[i, 0] != min_index:
                cluster_changed = True
            cluster[i, :] = min_index, min_dist**2
        print(centroids)
        # 更新质心的位置，直到簇分配结果不再改变为止
        for cent in range(k):
            index = cluster[:, 0].A # 簇分配结果中的所有索引
            value = nonzero(index == cent)
            sample_in_cent = dataset[value[0]]
            centroids[cent, :] = mean(sample_in_cent, axis=0) # 按列计算均值
    return centroids, cluster

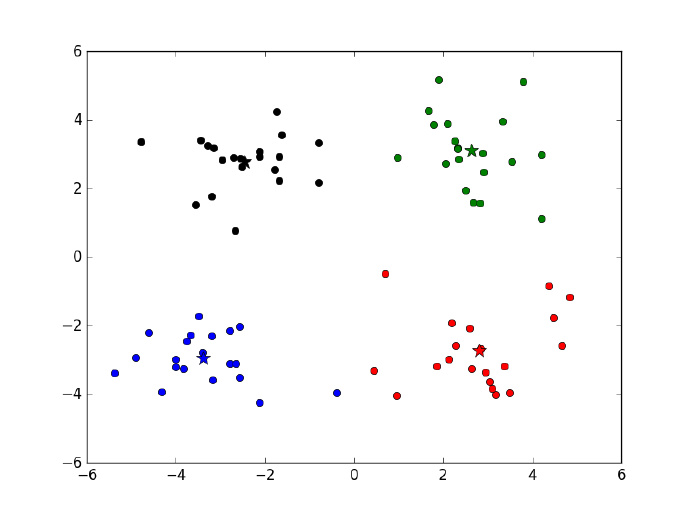
经过四次迭代之后算法收敛，得到 4 个质心，四个质心以及原始数据的散点图在下图给出。

[[ 1.71514331  4.38373482]
 [-2.07697989 -2.34923269]
 [ 1.37232864 -1.69241204]
 [-4.4940993  -0.98212537]]
[[ 1.21336621  3.14825539]
 [-2.98849186 -3.14785829]
 [ 2.8692781  -2.54779119]
 [-3.56936853  0.80979859]]
[[ 1.98283629  3.1465235 ]
 [-3.38237045 -2.9473363 ]
 [ 2.80293085 -2.7315146 ]
 [-2.768021    2.65028438]]
[[ 2.6265299   3.10868015]
 [-3.38237045 -2.9473363 ]
 [ 2.80293085 -2.7315146 ]
 [-2.46154315  2.78737555]]

def showCluster(dataset, k, centroids, cluster):
    numSamples, dim = dataset.shape
    mark = ['or', 'ob', 'og', 'ok']
    for i in range(numSamples):
        markIndex = int(cluster[i, 0])
        plt.plot(dataset[i, 0], dataset[i, 1], mark[markIndex])
    mark = ['*r', '*b', '*g', '*k']
    # 画出质心
    for i in range(k):
        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)
    plt.show()

k均值聚类的结果

三、如何选择合适的 K？

与其说为 k 均值选择合适的聚类数 k，倒不如说检验聚类的效果如何，因为 k 均值是无监督类的分析方法，所以在运用 K 均值算法的时候比较头疼的是我们事先无法知道最优的聚类个数。假定即使你事先确定了聚类的个数，而实际上也不一定能对应上，并且聚类的结果很大程度上依赖于分析人员喂给聚类模型的变量。在用 Spark 做 k 均值聚类时候通常有两个评估指标：

四、讨论

k 均值算法最大的优点就是运行速度快，在 Spark 上对 10W 条数据 190 个特征进行聚类分析，不到两分钟就可以跑完，速度还是非常快的，其实最主要的工作还是分析人员不断分析评估各种模型的好坏。但是它的劣势也是很明显的，比如它的区分度不是很好，对于稀疏数据的聚类，大多数的数据都集中在一块，无法剥离出来；到底 K 取多少需要分析人员不断尝试；另外，聚类分析需要用到什么变量也需要谨慎考虑，在聚类分析中我们应该使用与问题紧密相关的变量做聚类而不是使用所有的变量作为输入。

解决异常值敏感可采用 k 中心算法，k 中心点算法中，每次迭代后的质点都是从聚类的样本点中选取，而选取的标准就是当该样本点成为新的质点后能提高类簇的聚类质量，使得类簇更紧凑。该算法使用绝对误差标准来定义一个类簇的紧凑程度。另外的优化手段还有凝聚的与分裂的层次聚类。

参考

  1. 腾讯QQ大数据：用户增长分析——用户分群分析
  2. Clustering - Spark 2.4.0 Documentation

十一、K 近邻

k 近邻（knn）是一种很简单的分类算法，它的基本原理是：给定一个实例点，然后在所有的数据中找到与该实例点距离最近的 k 个样本，最后选择 k 个样本中出现最多的分类标记作为实例点的分类预测结果。

下面这个视频比较清晰地说明了 knn 是如何工作的：How kNN algorithm works - YouTube

基本的原理很简单，所以它很“懒”，是“懒惰学习”代表，它遗留了两个问题给我们思考：

  1. k 值如何选择？
    • k 值的选择不能过小，否则实例点会对自己周边的点异常敏感，容易过拟合
    • k 值的选取也不能过大，容易产生较大的误差
    • 一般选择一个合适的 k 值，用交叉验证法择优选取
  2. 如何定义实例点与样本点之间的距离？
    • 欧式距离
    • $L_p$ 距离，p=1 时为曼哈顿距离
    • 闵可夫斯基（Minkowski） 距离
  3. 如何快速找到实例点距离最近的 k 个样本？

关于问题 3 的回答，kd 树是 knn 的实现算法之一，参考【数学】kd 树算法之详细篇

kd树搜索过程

十二、梯度提升决策树

1. GBDT与AdaBoost的联系与区别

在前面的文章中，我们了解到了一种提升方法 —— AdaBoost ，它是一类能够从训练数据中学习一组弱分类器，并将弱分类器组合成强分类器的算法，通俗一点解释就是“三个臭皮匠顶个诸葛亮”。GBDT 跟 AdaBoost 一样都属于集成学习中的提升方法（另一种是 Bagging），特殊之处在于 GBDT 的弱学习器限定为了决策树（分类树或回归树），提升树可以看做是多颗决策树的线性组合。不过 AdaBoost 算是年代比较久远的集成学习算法，现在基本上很少用到了。

除了弱学习器的不同，另外，它们两者在迭代上有所区别。AdaBoost 利用的是上一轮学习器的误差率来更新数据的权重，在每一轮的迭代中误分类的数据和分类误差率小的模型会获得更高的权重，理论上 AdaBoost 的学习器可以选择任何分类模型，只是由于树形模型比较简单且容易产生随机性所以通常被用于基分类器。而 GBDT 的基学习分类器限定只能是 CART 回归树，顾名思义，它可以解决回归和分类问题，GBDT 的迭代思路是使用前向分布算法，基本思想是根据上一轮学习器损失函数的负梯度来训练本轮的学习器，本轮学习器 $f_{t}(x)$ 的优化的目标是将上一轮学习器的损失函数 L 优化得到一个最小值。如果这样解释还不太清楚，那我举一个例子，比如现在给你 k 次机会猜测我的真实年龄，并且下一次猜测的数字需要跟上一次猜测的数字相加才能成为下一次猜测的最终结果，第一次你猜测 20 岁，我说小了，然后第二次你说加 10 岁，我说大了，然后第三次你说减 5 岁，我说小了……

而如何拟合 GBDT 的损失函数则是一个 GBDT 需要考虑的关键问题。

总结一下 Adaboost 与 GBDT 的区别：

  1. Adaboost 是基于样本权重更新，误分类的样本和误差率低的学习器可以获得更高的权重
  2. Gradient Boost 是基于残差减小的梯度方向进行更新
  3. 理论上 AdaBoost 的分类器可以选择任何分类模型，GBDT 的学习器则限定于分类回归树

可以这样说，如果限定提升树的基分类器为分类回归树（CART），那么此时的GBDT 跟 AdaBoost 就没有差别了。

2. 回归问题的提升树算法

下面讨论回归问题的提升树，其实相比分类问题，回归问题更好计算，没有 AdaBoost 那一套复杂的权重更新过程，每一次的迭代只需要拟合残差，每一棵新树的建立都是基于残差的负梯度方向。残差是什么？残差是实际值与预测值之差：

$$ r = y_i - f(x_i) $$

打个比方，假设一个人真实年龄是 30 岁，第一颗回归树预测的结果是 27 岁，残差是 3，下一颗树的目标就是假定预测一个年龄等于 3 岁的人，如果第二棵树预测的结果是 2 岁，那么第一颗和第二棵树相加的结果 29 就是两棵树的预测结果。

回归问题的提升树有两个值得关注的点：

一、寻找使得残差最小的切分节点

二、平方损失误差 $L$ 达到要求后即可停止。

3. 梯度提升（Gradient Boosting）

上面一节中，可以知道，平方损失函数的情形很简单，但是对于更一般的损失函数，优化就没有那么简单了，于是我们需要在提升树算法中引入梯度下降的优化算法，即所谓的 GBDT。GBDT 的损失函数，如果是对于分类算法，其损失函数有对数损失和指数损失，如果是回归算法，其损失函数一般有平方损失、绝对值损失、Huber 损失函数（对异常值的鲁棒性比较强）等等。梯度下降优化算法的关键是计算其负梯度在当前模型的值，并将该值作为近似的残差，最后根据残差拟合一个回归树。

$$ -\left[ \frac{\partial L(y^{(i)}, f(x^{(i)}))} {\partial f(x^{(i)})} \right]{f(x) = f{k-1}(x)} \approx r_{m,i} $$

第 2（c）步的 $c_{mj}$ 是各个叶子节点最佳负梯度的拟合值，第 2（d）步将该拟合值更新到下一轮的学习器中。

4. sklearn GBDT 可调节的参数

按照分类和回归问题，sklearn 有 GradientBoostingClassifier 为 GBDT 的分类类， 而 GradientBoostingRegressor 为 GBDT 的回归类，两者的参数类型差不多相同。

  1. loss：选择损失函数，分类问题的损失函数可以选择对数损失函数（deviance）和指数损失函数（exponential），回归问题的损失函数可以选择均方差损失函数（ls）、绝对损失函数（lad）、huber 损失函数（huber）和分位数损失函数（quantile）
  2. learning_rate：学习率，默认 0.1，取值范围 (0,1]，文档提示这个参数经常需要跟 n_estimators 一块调节
  3. n_estimators：学习器的迭代次数，一般可以把这个参数设置得大一点以获得更好的效果，默认是 100
  4. subsample：采样率决定数据中不放回抽样一定比率的样本拟合基学习器，抽样能减小方差防止过拟合，但是同时也会增加偏差
  5. max_depth：决策树的最大深度，默认为 3，max_depth 限制了数的节点个数，如果数据集的特征和数据量比较大可以把这个值调大一点
  6. min_samples_split：内部节点再划分所需要的最小样本数，可以取 int 或者 float，如果在划分的时候子树的节点数小于这个参数便不会继续划分
  7. min_samples_leaf：叶子节点所需要的最少的样本数，默认等于 1，可以取 int 或者 float
  8. min_weight_fraction_leaf：叶子节点最小的样本权重和，如果样本中有比较多的缺失值可以引进这个参数
  9. max_leaf_nodes：最大叶子节点数，默认为 None，可以防止模型过拟合
  10. min_impurity_split：节点划分的最小不纯度，如果节点的不纯度小于它，那么该节点不再生成子节点

5. GBDT 的优点和局限性

优点：

  1. 由于 GBDT 的弱学习器是决策树，这就决定了我们在应用模型的时候无需对数据进行归一化等预处理
  2. 泛化能力强

局限性：

  1. 不适合处理文本分类的任务，在高维稀疏的数据集上表现也一般
  2. 因为 GBDT 是加法模型，下一个模型是基于上一个模型的，所以它的训练过程是串行的

6. 推荐阅读

  1. 机器学习中的算法(1)-决策树模型组合之随机森林与GBDT
  2. chentianqi: XGBoost 与 Boosted Tree
  3. GBDT原理与Sklearn源码分析-分类篇 - SCUT_Sam - CSDN博客
  4. GBDT原理与Sklearn源码分析-回归篇 - SCUT_Sam - CSDN博客

十三、AdaBoost

在 Adaboost 中会有很多次的迭代计算，每一次的迭代计算得到一个基本分类器，根据已有的基本分类器，Adaboost 算法会提高那些在前一轮被弱分类器误分类的样本的权值，并降低那些被正确分类的样本的权值，对于“差生”重点关注。提升方法通过重复修改训练数据的权重分布，构建一系列的弱分类器，然后依据特定的组合算法对这些弱分类器进行线性组合，从而得到最终的强分类器。

Adaboost 是一个“笨蛋”，一开始它也许不怎么聪明，但是它非常乐于改进并接受他人的意见，所以最后它会变得很强大。

偏差指的是模型的期望预测值与真实结果的偏离程度，Boosting 方法在训练的过程中非常关注自己在每次的训练中所犯下的错误，所以“从偏差-方差分解的角度看，Boosting 主要关注降低偏差，因此 Boosting 能给予泛化性能相对弱的学习器构建很强的集成”。

一、背景

在机器学习中，集成学习（Ensemble learning）目标是构建并组合多个学习器（Weak learner）来完成学习任务，组合学习器中的单个学习器“单兵作战”的效果可能并不理想，然而多个这样的学习器组合起来效果就很可观了。有一句俗话，“三个臭皮匠顶个诸葛亮”，意思是说几个资质平庸的人联合起来也有能有大智慧，集成学习的道理也是如此：能力不够，人头来凑。

集成学习

学习一个简单粗糙的弱学习器比学习一个准确率很高的学习器要简单得多，比如预测股市的涨或者跌，没有任何知识背景的外行瞎蒙也有 50% 的准确率。然而通过特定组合算法的学习，这样几个弱学习器最终学习器整体的性能却能够得到显著提高，这个提高的过程也被称为提升（boosting）。提升是集成学习的一类，可以理解为“集思广益”，即团结力量大。这篇文章要介绍的便是集成学习中一个非常著名的算法—— Adaboost 算法。

二、Adaboost 算法

Adaboost 算法的原理比较简单，在 Adaboost 算法中，有两个难点问题需要弄明白：

Adaboost 算法的基本思路大致有 3 个步骤，首先 Adaboost 给予训练集中的每个样本均匀的权重 $w_{1i}=\frac{1}{N}$，即每个训练样本在 $h_{1}(x)$ 分类器中所起得作用均一样；然后 Adaboost 反复学习 $h_{1}(x)$ 分类器，分别更新数据集权重和 $h_{m}(x)$ 分类器的系数；最后组合 $m$ 个弱学习器得到最终分类器。

Adaboost 算法

  1. 初始化训练数据 $T$ 的权重分布 $D_m$； $$ D_1 = (w_{11}, w_{12},…,w_{1N}), w_{1i}=\frac{1}{N} $$

  2. 基于初始化训练数据集进行学习，得到弱学习器 $h_{1}(x)$；

  3. 对 $m=1,2,..M$，计算弱学习器 $h_{m}(x)$ 在训练数据集上的误差率 $e_m$ 和弱学习器 $h_{m}(x)$ 的系数 $\alpha$；

    $$ e_m = P(h_{m}(x) \neq y_i) $$ $$ \alpha_m = \frac{1}{2}\ln\left(\frac{1-e_m}{e_m}\right) $$

  4. 更新训练数据集的权值分布，迭代到第 $m$ 次时； $$ D_{m+1} = (w_{m+1,1}, w_{m+1,2},…,w_{m+1,N}) $$ $$ w_{m+1,i} = \frac{w_{m,i}}{Z_m}\exp(-\alpha_{m}y_ih_{m}(x_i)) $$ $$ Z_m = \sum_{i=1}^{N}\exp(-\alpha_{m}y_ih_{m}(x_i)) $$

  5. 构建弱学习器的线性组合，得到最终分类器 $G(x)$

    $$ f(x) = \sum_{i=1}^{N}\alpha_{m}h_{m}(x_i) $$ $$H(x) = sign(f(x))$$

三、Adaboost 算法参数的解释

不打算继续深究的读者可以就此打住了，毕竟大多数人只是用用模型，背后复杂的数学推导根本没有必要。然而，本着知其然更要知其所以然的精神，我们还是有必要对 Adaboost 算法中涉及到的两个点——弱学习器系数和数据集权值分布，做一个简单的梳理，亦呼应了上一节开头提的两个问题。

1. 分类器权重 $\alpha_m$ 更新原理

Adaboost 算法的优化目标是最小化指数损失函数

$$ \begin{aligned} E &= \exp(-f(x)H(x)) \ &= \exp(-f(x)\alpha_mh_m(x)) \ & \quad \text{（} f(x)h_m(x) \text{ 只有 } 1 \text{ 和 } -1 \text{ 两种情形，同时对应两种概率）} \ &= \exp(-\alpha_m)(1-e_m) + \exp(\alpha_m)e_m \end{aligned} $$

对 $\alpha_m$ 求导并令其为零可得分类器权重更新公式

$$ \alpha_m = \frac{1}{2}\ln\left(\frac{1-e_m}{e_m}\right)$$

2. 数据集权重 $\bar{w}_{m+1,i}$ 更新原理

求解在每一轮样本的权值更新，由下面两个式子

$$f_m(x) = f_{m-1}(x) + \alpha H_m(x)$$

$$ \bar{w}{m,i} = \exp(-y_if{m-1}(x_i)) $$

得

$$ \frac{\ln(\bar{w}{m+1,i})}{-y_i} = \frac{\ln(\bar{w}{m,i})}{-y_i} - \alpha_m H_m(x)$$

经过化简可得样本权值的更新公式，对应算法中的权值更新公式，唯一的区别在与少了一个规范化因子，但是这并不妨碍与下式等价

$$ \bar{w}{m+1,i} = \bar{w}{m,i} \cdot \exp(-y_i \alpha_m H_m(x)) $$

3. 分类误差率 $e_m$

$$ e_m = \sum_{i=1}^{N} w_{m,i} I(h_{m}(x_i) \neq y_i)$$

Adaboost 算法的笔记暂时告一段落了，如果读者还有不太明白的地方，可以参照《统计学习方法》第 140 页的“Adaboost 例子”来辅助理解，文末提供的参考 5 给出了该例更为详细的讲解，相信对理解 Adaboost 算法的原理会有一定的帮助。

笔者是头一次接触集成学习（Ensemble learning），在这之前对集成学习的概念很是模糊，因为先前接触到的都是依据单个算法做成的分类器，所以一直弄不明白的是多个弱分类器是如何组成称为一个新的并且性能更强大的分类器。知其然还要知其所以然，笔者一直认为不管是直接调用各种强大的库，还是调一调参数以期提高机器学习的应用水平，背后的数学原理还是有必要去理解一下的，不然总有一种不踏实的感觉。

参考

  1. 统计学习方法.李航
  2. 机器学习.周志华
  3. Explaining AdaBoost
  4. Adaboost - 新的角度理解权值更新策略
  5. Adaboost 算法的原理与推导（读书笔记）

十四、XGBoost

XGBoost 是 GBDT 的一种高效的实现，它是由华盛顿大学的陈天奇开发的一个高度可扩展的、端到端的提升系统。近几年 XGBoost 在各大算法竞赛中取得的成绩一时间可谓风头无两，它取得成功背后在于它在所有场景中的可扩展性，它在处理稀疏数据上的标点也是非常强大的。

1. 回顾提升树（Boosting Tree）

提升树（Boosting Tree）是集成学习的代表之一，在之前的文章中我们就提到过，集成学习的本质：单个单个的基学习器表达能力弱没有关系，只要把它们组合起来了就可以很强大了，可以概括为“三个臭皮匠顶个诸葛亮”。

提升树实际上是 K 个弱学习器的线性组合而得到的加法模型，所谓提升（Boosting）的本意是在上一个弱学习器的基础上更进一步缩小与目标值的距离，使用公式可以表示为（来自陈天奇的论文）：

简单解释一下，数据集中的每一条数据都会落入弱学习器叶子结点的某一个区域，即对应的预测值，然后最终的预测结果等于所有树的预测值之和。如下图，小男孩（代表数据集中的一条数据）最终的预测结果为 tree1 和 tree2 预测值之和：

2. XGBoost 损失函数的优化求解过程

以上就是对提升树模型的简要回顾，下面正式进入 XGBoost 的部分，首先看 XGBoost 的损失函数：

回顾 GBDT 的损失函数：

可以看出，相比 GBDT，XGBoost 在其基础上添加了正则化项 $\Omega(h_t) = \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$，正则化项中的 $w_{tj}$ 对应第 $t$ 个弱学习器第 $j$ 个叶子节点的最优值，与 GBDT 损失函数中的 $c$ 是相同的意思（陈天奇的论文中是用 $w$ 表示的，意思一样），$J$ 指的是叶节点的个数，$\gamma$ 和 $\lambda$ 都是超参数。在损失函数中添加正则化项的有助于降低模型的复杂性和防止模型出现过拟合的情况。

接下来问题来了，如何最小化 XGBoost 的损失函数呢？对于公式（2），如果节点的分裂使用的是均方误差那很好优化，而 XGBoost 损失函数却无法通过一般的凸优化方法来求解，因为它实质上是一个 NP hard 的问题，因此 XGBoost 使用的贪心法来获得优化解，每次节点的分裂都期望最小化损失函数的误差，所以 XGBoost 的损失函数中加入了当前的树 $f_t$，损失函数变成：

然后对该损失函数做泰勒的二阶展开得：

其中 $g_i$ 和 $h_i$ 是第 i 个样本在第 t 个弱学习器对 $\hat{y}^{(t-1)}$ 一阶偏导和二阶偏导，由于损失函数中的 $l$ 是常数，在最小化中可以去掉，上面的式子可以进一步写成：

以下是公式（4）的推导改写过程，将 n 条数据全部代入目标函数后，可以将式子从叶节点的角度改写一下

对于公式（4）的 $w_j$ 的求解比较简单，损失函数对 $w_j$ 求导并令其为 0，可得最优解 $w_j^{*}$：

然后将最优解代入公式（4），可得：

接着，每次在节点做左右子树分裂 split 的时候，我们要尽量减少损失函数的损失，也就是说，假设当前节点左右子树的一阶、二阶导数和为 $G_L,H_L,G_R,H_R$，我们期望最大化下式（为什么是期望最大化下面会解释）：

整理，得：

这里有一个疑问，上面的这个式子是怎么从公式（6）计算得来的呢？自己想了很久没有想清楚，在 B 站上找到了一个 up 主把节点分裂的过程解释得非常到位！看下图，现在假设我们有从 1 到 8 的 8 个样本点。

第一次分裂，左子树两个样本点 {7,8}，右子树有六个样本点 {1,2,3,4,5,6}，此时的目标函数为：

接下来，我们选择某个特征对右子树做节点分裂，假设分裂的结果为左子树为 {1,3,5}，右子树为 {2,4,6}，此时的目标函数为：

在节点向下分裂的过程中，我们希望第二步目标函数变得越来越小，故实际上我们期望最大化的是第一步的目标函数减去第二步的目标函数：（这里请重点理解！）：

到此，XGBoost 损失函数的优化求解就记录得差不多了。

3. XGBoost 的训练过程

  1. 计算所有 m 个样本对于当前轮损失函数的一阶导数 $G$ 和二阶导数 $H$
  2. 基于当前节点分裂决策树，初始化 score 为 0，如果当前有 $k$ 个特征：
    1. 样本按照第 k 个特征排好序，放入左子树，然后计算左右子树一阶和二阶导数和
    2. 更新 score
  3. 基于 score 最大的特征分裂

4. XGBoost 类库的参数

在梯度提升决策树 的文章的末尾提到了 GBDT 在 sklearn 中可以调节的参数，其实 XGBoost 和 GBDT 可调节的参数都差不多。

通用参数：

  1. booster ：弱学习器种类，gbtree 或者 dart
  2. objective：损失函数，如果是回归问题一般使用 reg:squarederror，分类问题使用 binary:logistic 或者 multi:softmax，另外还可以通过设置损失函数决定模型的输出是概率还是原始的预测值
  3. n_estimators：弱学习器的个数，决定了模型的复杂程度，通常和学习率参数一块调参

弱学习器参数：

  1. eta [default=0.3, alias: learning_rate]：学习率，默认等于 0.3
  2. gamma [default=0, alias: min_split_loss]：等于目标函数中正则化项的 gamma，决策树分裂时最大化下式时必须大于 gamma 才能继续分裂
  3. max_depth [default=6]：定义树的最大深度，决定了模型的复杂程度，通常需要通过网格搜索决定最佳的树的深度
  4. min_child_weight [default=1]：决策树中子节点最小的权重阈值，如果子节点的权重阈值小于 min_child_weight 则不再继续分裂
  5. subsample [default=1]：训练集的采样率，介于 0,1 之间
  6. sampling_method [default= uniform]：采样方法，有 uniform 和 gradient_based
  7. colsample_bytree, colsample_bylevel, colsample_bynode [default=1]：针对特征采样的手段，层级别、树级别和子节点级别，采样率介于 0,1 之间
  8. lambda [default=1, alias: reg_lambda]：L2 正则化系数，对应 $\Omega(h_t) = \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$ 里面的 $\lambda$
  9. alpha [default=0, alias: reg_alpha]：L1 正则化系数，对应 $\Omega(h_t) = \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$ 里面的 $\gamma$
  10. tree_method：默认 auto，自动选择最快的方法

参考：Python API Reference — xgboost 1.5.0-SNAPSHOT documentation

5. GBDT 和 XGBoost 的区别与联系：

  1. GBDT 是集成学习算法，而 XGBoost 是 GBDT 的一种高效工程实现
  2. 对比 GBDT 的损失函数，XGBoost 还加入了正则化部分，防止过拟合，泛化性能更优
  3. XGBoost 对损失函数对误差部分同时做了一阶和二阶的泰勒展开，相比 GBDT 更加准确
  4. GBDT 的弱学习器限定了 CART，而 XGBoost 还有很多其他的弱学习器可以选择
  5. GBDT 在每一轮迭代的时候使用了全部的数据，而 XGBoost 采用了跟随机森林差不多的策略，支持对数据进行采样
  6. GBDT 没有设计对缺失值的处理，XGBoost 能够自动学习出缺失值的处理策略

参考：

  1. XGBoost算法原理小结 - 刘建平Pinard - 博客园
  2. XGBoost的技术剖析_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
  3. https://arxiv.org/pdf/1603.02754.pdf

十五、随机森林

为了得到更强的泛化性能，在集成学习中我们期望个体学习器尽可能不相同，因为只有这样才能够全面地概括数据，所以有了 Bagging 这个方法。Bagging 是并行式集成学习方法的代表，它基于自助采样法（Bootstrap sampling），给定 m 个样本的数据集，有放回地抽取一个数据作为数据集，重复 m 次随机采样得到 m 个样本的数据集。然后，我们可以将以上的步骤重复 T 次，得到 T 个大小为 m 的随机样本数据集，基于每个样本数据集训练学习器。最后，针对是分类或者回归任务使用投票或者平均来确定最终学习器学习的结果。

随机森林在 Bagging 的基础上做了改进，随机森林会再次对特征做了一次随机选择，比如对于自助采样后的每一个子数据集（总共 m 个子数据集），我们并不会像决策数那样用到所有的特征，随机森林会从所有的特征中随机选择一个包含 k（k<n） 个特征的子集（通常 k 取 log2(n)）。当有一条新数据进来，在随机森林的 m 棵树会各自给出一个答案，如果是分类任务，我们就选择投票法，如果是回归任务则一般选择平均值作为输出。不像决策树，越靠近根节点的特征重要性越高，在随机森林中，在每个特征都是有可能成为“主角”的，也不容易出现过拟合的问题，可以说泛化的优点很明显。

选取特征子集

看了很多资料，似乎大家都把随机森林理解得有点复杂，推荐大家观看一个印度人的讲解视频：What is Random Forest Algorithm? A graphical tutorial on how Random Forest algorithm works? - YouTube ，很清晰明了。

十五、卷积神经网络

写在前面

没想到博客能存活到现在，全凭着一股兴趣，不知不觉这个系列已经写到第 13 篇了。一直以来，我都是抱着初学者的心态来写机器学习算法，限于专业以及其他因素，圈子内有同样兴趣的伙伴少之又少，所以对机器学习的理解大多来自独自阅读论文和观看教学视频，个人的理解难免出现低级错误。再加上本人又非科班出身，遇到难以理解的地方往往“求告无门”，只能翻来覆去的啃，铺天盖地地搜，难免陷入主观的境地。

本文主要写的是笔者对 CNN 原理的一些个人理解，在 CNN 如何进行学习以及 dropout 没有做太多涉及，笔者接触卷积神经网络（Convolutional Neural Network，以下称 CNN）的时间不长，不论是看的论文还是做的 project 都远远不够，出现错误在所难免，理解上出现的偏差我是要负主要责任的，欢迎大家帮我找出文章中纰漏！

Regular Neural Nets don’t scale well to full images.

在之前的一篇文章中：机器学习算法系列（8）神经网络与 BP 算法 ，我们了解到对于一般神经网络，它们的基本组成结构分为输入层、隐藏层和输出层三个部分，隐藏层分布的各个神经元彼此独立，他们各自从输入层接受输入并进行计算，汇总之后再传送至输出层；还有反向传导算法的实现过程。

理论上，参数越多的模型复杂度越高，同时也能够完成更加复杂的学习任务，但是与此同时参数过多造成许多不足。通常，一般神经网络会面临参数剧增的问题，比如神经网络的输入为一个 $[255, 255, 3]$ 的矩阵，完全展开后即为 $172,125$ 维的向量，假设隐藏层有 $1,000$ 个神经元，那么仅仅从输入层到第一层隐藏层参数的个数就达到了 $255 \times 255 \times 3 \times 1000=172,125,000$ 个！是不是有点恐怖？如果再向神经网络添加几个隐藏层，参数数量上升的速度会非常快，从而在计算上将变得十分耗时（近年来深度学习大热，与计算机计算能力大幅提升的背景离不开），并且参数数量过多还容易导致模型的过拟合。而 CNN 通过参数共享（shared weights）、下采样（sub-sampling）等手段能够较好地克服了一般神经网络中参数剧增的缺陷。

1. CNN 结构的解释

1.1 卷积、池化、全连接

在理解 CNN 的结构之前，有必要了解几个基本的概念：卷积（Convolution）、池化（Pooling）和全连接（Fully-Connected），将这三种不同的层按照一定的结构连接起来便组成了卷积神经网络的基本架构。

卷积

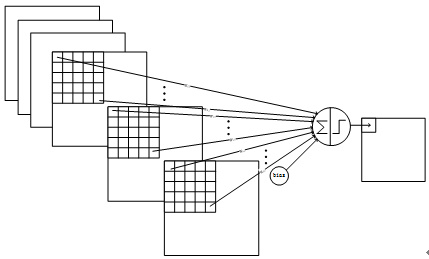
“自然图像有其固有特性，也就是说，图像的一部分的统计特性与其他部分是一样的”，也就是说图像或者是向量化后的文字同样具备一定的统计特性，即同样也可以进行特征提取、组合。在 CNN 中，卷积运算便是这么一个过程，不同于拥有显示特征的数据，CNN 对数据的特征提取是通过 filter 来进行的，每个 filter 都有着采集不同的特征的任务，因此 filter 中参数的大小是不相同的。

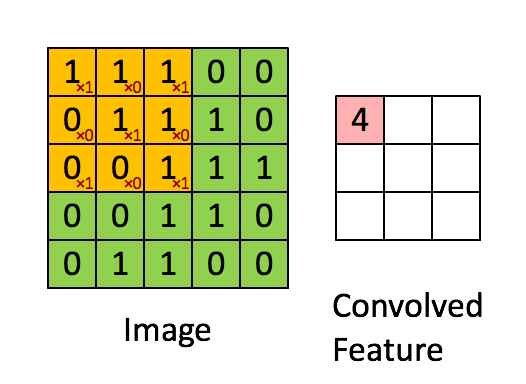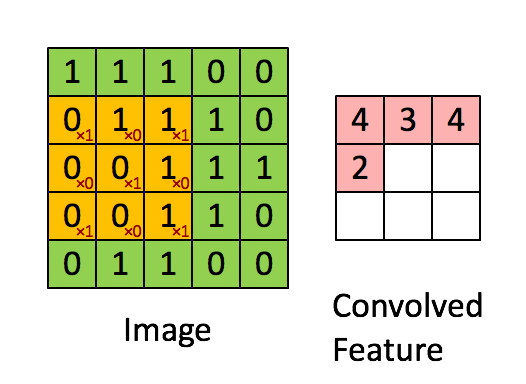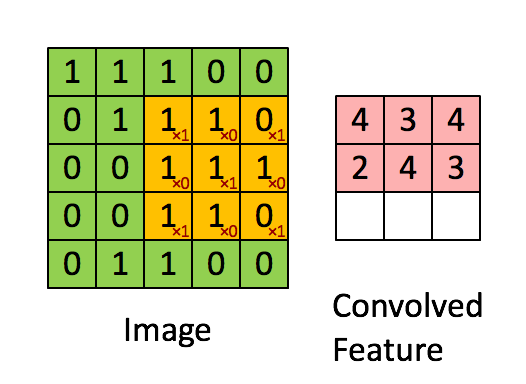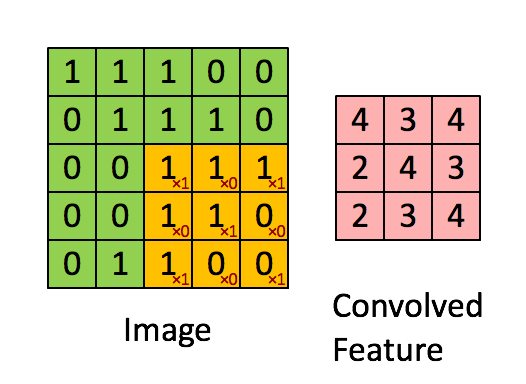
3×3 的 filter 从左至右从上至下以步长为 1 依次遍历整个图像得到一个 3×3 大小的 feature map

以识别图像中的小鸟为例，有的 filter 可能专门找像鸟嘴的部分，有的则专门找寻找像鸟的尾巴的部分，并且 feature map 会共享（sharing）来自 filter 的参数。

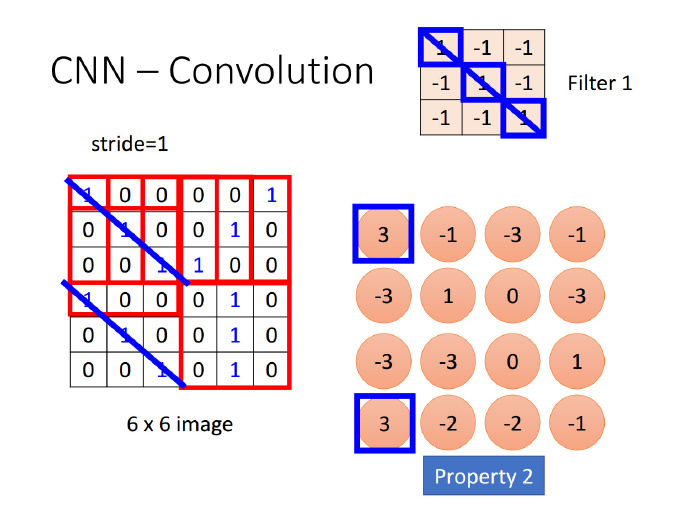
Filter 1 会专门找 image 中斜对角都为 1 的部分

池化

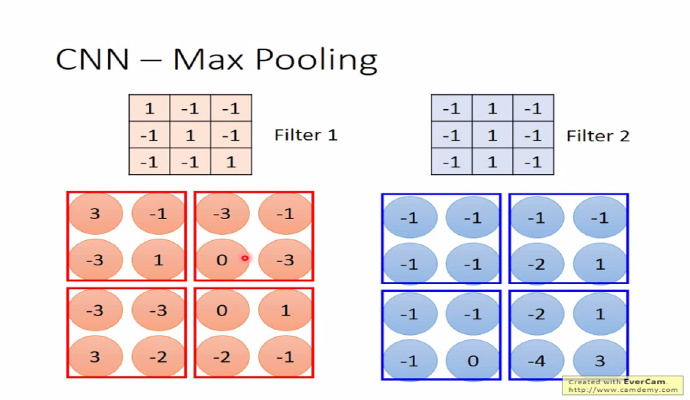
池化的目的是为了减轻计算量的压力，池化还有一个作用，它能够使模型具备识别平移、转换、缩放图片的功能@杨培文。比如对于一个 $32 \times 32$ 的图像，如果经过 $100$ 个 $5 \times 5$ filter 卷积提取得到 $100$ 个 $(32-5+1) \times (32-5+1)=784$ 维的卷积特征，那么对于每个输入都有 $78,400$ 维度的卷积特征向量，这个给计算带来了巨大的压力。 为了解决这个问题，池化的方法比较简单，可以理解它是一个采样的过程，对 filter 过滤出来的 feature map，我们可以将它分成几个小块，然后对每个小块采取**取最大（max pooling）或取平均（average pooling）**的操作，从而达到降维的目的。

CNN Max pooling

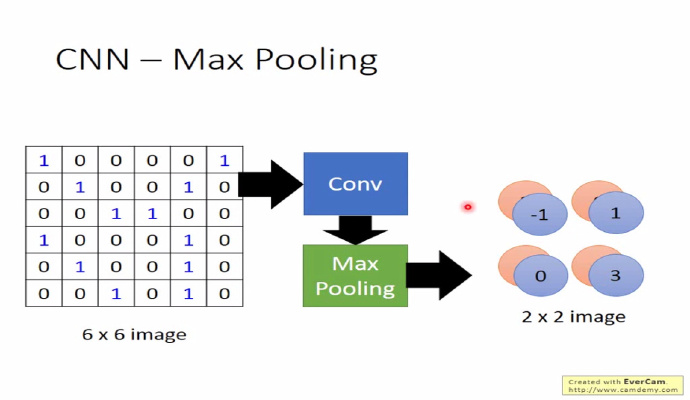
然后 CNN 反复重复 Conv->Pooling 的这个过程，最后展开（flatten）连接到全连接层。这时参数个数便能够下降到可以接受的范围之内。

1.2 卷积层、池化层大小的计算

无论是卷积到池化还是池化到卷积，两个过程的参数个数计算其实区别不大。

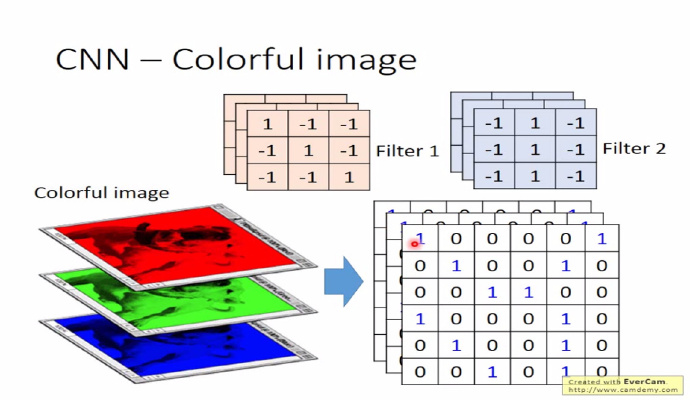
如果输入层有 $n$ 个 channel，滤波器（filter）会考虑到 channel 的深度，那么滤波器的结构一般也是（$* \cdot * \cdot n$）的结构；filter 的个数决定了卷积层的深度 $D$ 和 feature map 的个数。

如下图，如果输入的图像有 RGB 3 个 channel，相应 filter 的结构也为 $* \cdot * \cdot 3$。

filter size

filter 的结构为3×3×3，得到两个 feature map

零填充（zero padding）个数有助于适应 filter 和控制输出单元的大小

1.3 例子

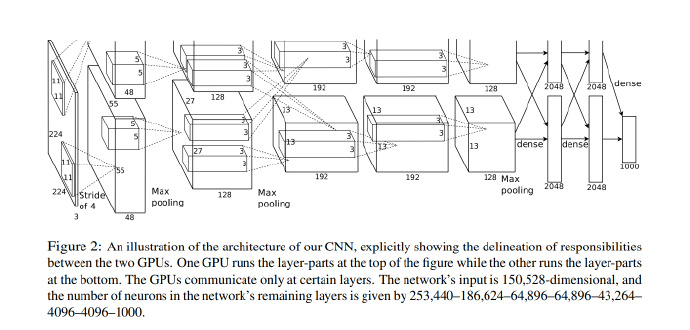
举个例子，赢得 2012 年 ImageNet 的 Krizhevsky et al. CNN 架构中接受的是 $[227 \times 227 \times 3]$ 大小的图片（原文中是说 $224 \times 224 \times 3$，但这样计算得到的卷积层大小不是一个整数，应该是作者使用了零填充但是却忘了在文中提及），一共有 $K = 96$ 个大小为 $[11 \times 11 \times 3]$ 的滤波器，$F = 11$，步长 $S = 4$， 那么卷积层计算 $(227 - 11+0)/4 + 1 = 55$，卷积层的大小便为 $[55 \times 55 \times 96]$。

ImageNet Classification with Deep Convolutional Neural Networks

2. 经典的 LeNet-5

若要提起 CNN，就不得不提起 Yann LeCun 用 CNN 进行手写数字识别任务的论文，LeCun 这篇经典论文的插图在各种文章中被引用了无数遍，相信你也不是第一次在这里看到这幅图片

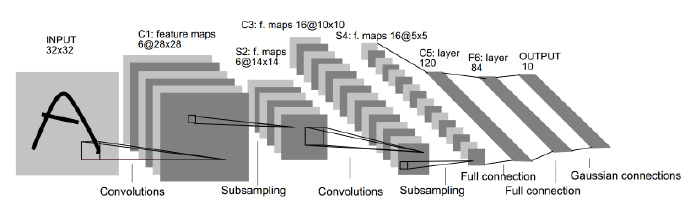
LeNet-5, a Convolution Neural Network

如上图所示，不包括输入层（Input layer），LeNet-5 网络一共有 7 层，分别是 3 个 卷积层（Convolution layer），2 个采样层（Subsampling layer），1 个全连接层（Fully-Connect layer）和 1 个输出层（Output layer）。

LeNet-5 的输入层是 $32 \times 32$ 的手写数字图像的像素矩阵，输出层是长度为 10 的向量，分别对应 10 个数字相应的概率。$Cx$ 表示卷积层，$Sx$ 表示采样层，$Fx$ 表示全连接层（$x$ 表示层的索引）。Lenet-5 经过两轮的卷积（Convolution）、采样（Subsampling）重复操作，$32 \times 32$ 的输入被整合为 16 个 $10 \times 10$ 的矩阵，最后经过两个全连接层到达输出层。

C1

C1 卷积层有 6 个 feature map，这 6 个 feature map 分别由 6 个 $5 \times 5$ 的 filter 过滤得来。算上偏置项（bias），从输入层到卷积层中间有 $(5 \times 5+1) \times 6 = \textbf{156}$ 个可以训练的参数（trainable parameter）（对比一般神经网络，参数数量根本不是一个数量级）和 $(28 \times 28 \times 6) \times (5 \times 5+1) = \textbf{122,304}$ 个连接。

S2->C3

S2 采样层共有 12 个参数和 5880 个连接。

采样层参数个数解释

C3 卷积层有 16 个 feature map，上面讲过有多少个 filter 就有多少个 feature map。显然，S2 采样层到 C3 卷积层之间有 16 个 filter，与 C1 卷积层一样，每个 filter 的大小为 $5 \times 5$。然而，C3 卷积层的参数个数计算稍微有点绕，LeCun 在原文中的解释如下图：

LeCun 论文中的解释

原文大意是：前 6 个 feature map 从采样层相邻的 3 个子集获得输入，接下来的 6 个 feature map 又从采样层相邻的 4 个子集获得输入，剩余的 feature map 也依照这种办法生成。为什么要采用这种方法来生成 feature map 呢？LeCun 解释有两个方面的原因，首先这种不完全的连接（non-complete connection）能够保证连接数能被控制在一定的范围之内，再者便是它能够强行打破网络的对称性（symmetry in the network），不同的 feature map 能较好地提取不同的特征。

通过下面这幅图以前 6 个 feature map 从采样层相邻的 3 个子集获得输入为例，只不过这里单个生成 feature map 的 filter 是由三个 $5 \times 5$ 的矩阵联合组成的。

从 S2 到 C3 总共有 1,516 (456+606+303+151) 个可训练的参数，每个 filter 连接的都是 $10 \times 10$ 的 feature map，那么全连接数即为 151,600 个。

$$ \begin{aligned} (553+1)6=456\ (554+1)6=606\ (554+1)3=303\ (55*6+1)*1=151 \end{aligned} $$

S4->C5

S4 是有 16 个 $5 \times 5$ 大小 feature map 组成的采样层，由上面的算法，一共有 32 个可训练的参数和 2,000 个连接。

C5 卷积层拥有 120 个 feature map，因为 C5 卷积层的 feature map 是 $1 \times 1$ 的，所以 S4 与 C5 之间的连接是全连接，将 S4 铺平展开为一个 $400 (5 \times 5 \times 16) \times 1$ 的矩阵，则可训练参数的个数为 $400 \times 120+120 = \textbf{48,120}$ 个。

终于到 F6 全连接层了，全连接层有 84 个单元，与 C5 卷积层 fully connected 之后，它们之间一共有 10,164 个参数。

以手写数字识别为例，CNN 的输出有十个单元，对应 F6，不难得出全连接层到输出层有 840 个连接，840 个可训练的参数。

以上就是 LeNet-5 的卷积神经网络的完整结构解释，网络中共计 60,840 个训练参数，340,908 个连接，参数和连接数统计表格总结如下：

卷积-采样 训练参数 连接数
input->C1 156 1,122,304
C1->S2 12 5,880
S2->C3 1,516 151,600
C3->S4 32 2,000
S4->C5 48,120 48,120
C5->F6 10,164 10,164
F6->output 840 840
总计 60,840 340,908

3. CNN 是如何学习的？

在接触 CNN 的过程中，似乎感觉其解释性不够强，给人一种“黑盒”的印象。简单讲讲 CNN 是如何进行学习的？以数字识别为例，专门寻找数字 8 弯弯曲曲特征的 filter 过滤生成了 feature map，把 feature map 的每一个元素相加得到 $a^k$，表示 filter 被刺激的程度，CNN 的任务便是寻找一张能够使 $a^k$ 最大的 image $x$。

$$ a^k = \sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}^k $$

$$ x^* = \arg \max a^x (gradient\ ascent) $$

4. CNN 在文本分类中的表现

CNN 非常强大，在文本、图像分类上尤为突出，即使没有做任何数据预处理的操作，简单的模型也能得到很好的效果。

…..Despite little tuning of hyperparameters, this simple model achieves excellent results on multiple benchmarks……

简单说一下 Kim, Y. (2014). 的这篇文章，作者在实验时直接用了 Mikolov 从 Google News 1000 亿个单词中预训练好的词向量，通过 CNN 来做句子层面的分类任务，并得到了非常理想的结果。思路如下：假设词向量 $x_i$ 为 $k$ 维向量，（$k$ 等于句子的最大长度，这样才能保证输入的矩阵维度一致），$x_i$ 对应着句子中的第 $i$ 个词，如此一来，一个长度为 $n$ 的句子便可以表示为 $n \times k$ 的矩阵，这么一来句子便可以进行向量计算了！（不得不佩服 Mikolov，他是怎么想到 word2vec 这个办法的）。

接下来的步骤便是依葫芦画瓢了，卷积提取特征，从 feature map 中选择一个最大值，进入全连接层，最后得到输出。实验结果如下，CNN 在 7 个语料库上有 4 个的准确率超过了传统方法。

5. Summary

如何理解 CNN？从人的经验角度来看，正如我们人识别动物，人们不会把动物仔仔细细看个遍才做出判断，而是看到小鸟有尖尖的嘴巴、羽毛、流线型的身体等等几个特征就能够分辨是不是小鸟。卷积神经网络的工作原理也类似，神经元不会像一般神经网络一样去傻傻地去遍历整张图片来提取特征，而是只需要看一小部分就行了，每个神经元都有自己独特的任务，如下图所示，神经元主要的任务是识别小鸟的嘴巴。

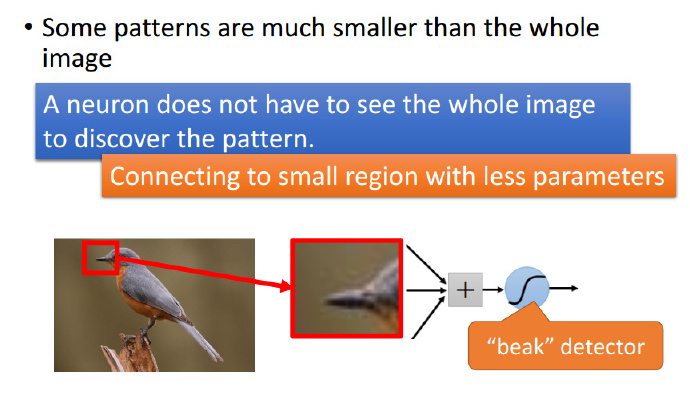
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html

有人可能会问，如果小鸟的嘴巴没有在图片中央而是在右上角，是不是又需要一个专门识别右上角小鸟嘴巴的神经元呢？答案是否，相同特征可能会出现在图像中不同位置，在 CNN 中，这些发现相同特征的神经元彼此之间是共享参数的，实际上它们做的是同一件事情。

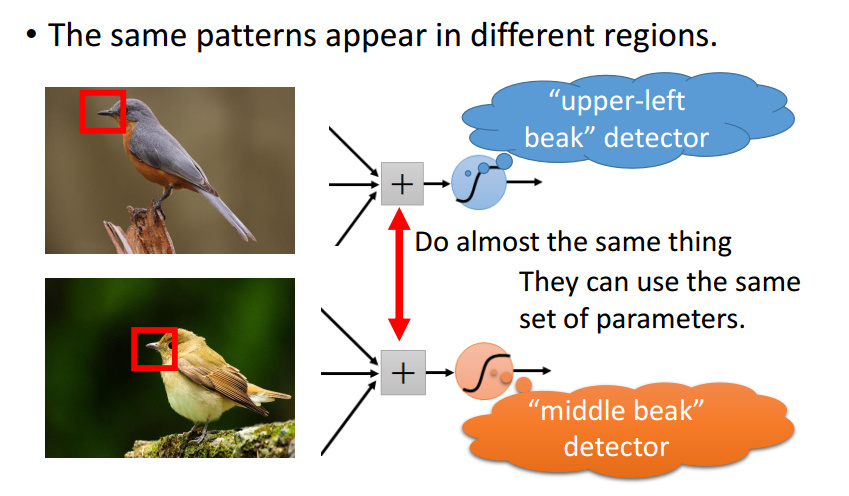
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html

随着 CNN 层数的叠加，越往后面提取的特征越发抽象难以理解，还有如果特征太多了怎么办？那我们就取一小部分就好了。

你能猜到这是谁吗？图片来自网络

池化的直观理解：去除图片的一部分有时候并不会影响对整个图片的理解。

http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html

在 CNN 中防止模型出现过拟合一般有 data augmentation 和 dropout 两种手段，前者是人工地增加数据量，后者是随机地让某些神经元失效，以达到减少参数量的效果。

十六、LSTM

先前仅仅是听 RNN 这个名词比较多一点，但没有深入去了解，在前一篇文章中我用CNN做了一次文本分类的实践 ，然后发现 RNN 也可以完成该任务，所以便开始寻找相关资料学习 RNN。我比较推荐台大李宏毅老师的机器学习课程，算是比较清晰易懂的了，没有公式堆砌，完全“人肉手撕”。课程里面有两节专门讲解 RNN，第一节讲原理（认真看），第二节讲应用的场景（快速过）。

学完课程，对照 PDF 课件差不多知道了 RNN 相比传统的神经网络具有“记忆”的特性，更加注重数据的上下文关系，就不难理解现有语音识别、机器翻译、自动生成等等技术背后的知识，以及 RNN 最成功的扩展长短时记忆网络（简称 LSTM，Long Short-term Memory）。现在，我基本理解了 RNN 的一些知识，以笔记的形式记录下来。

神经网络比较

回想先前接触的神经网络，前馈神经网络、DNN、卷积神经网络，它们都可以比较好地胜任器学习任务，比如文本分类，这些任务的有一个最大的特点：在建立训练模型的时候不用考虑各个输入之间的关系（上下文），输入与输入、输出与输出都是相互独立的。

现有一个新的场景，如下图，给定一段文字，需要从文字中提取地点和时间信息，用传统的神经网络可以解决，但是如果我们想知道地点到底是“出发”还是“目的地”就不可以了，因为输入“arrive”和“Taipei”之间是独立的，一般神经网络没有办法学习到它们之间的联系，这个时候就需要神经网络拥有“记忆”能力。

image

在 RNN 中会有一个记忆单元，它储存着隐藏层的输出，并把它当做下一次的输入之一。你有可能不明白，为什么是“输入之一”的表述，难道还有多个输入？是的，这就是 RNN 区别于普通神经网络的地方，上一次的输入对下一次的输入会有影响，正是如此它才拥有记忆力，假如你随意改变输入的序列顺序将会对 RNN 有很大的影响，一个说话颠三倒四的人不太好理解吧哈哈。

如果你不太理解，建议打开原来的视频看看李老师的教学视频，从 7:21 开始的地方有一个例子，看完就会理解 RNN 记忆单元的工作原理，本文就不再复述了。

image

LSTM 结构

上述是 RNN 最简单的一种形式，当然它还有很多扩展，其中最有名的便是长短时记忆网络，简称 LSTM。

长短时记忆网络，正确的断句应该是“长/短时记忆/网络”，字面意思是在 LSTM 中 RNN 会拥有比较长的短时记忆，由遗忘门控制。

相比最简单的 RNN，控制 LSTM 记忆单元（memory cell）有 3 个 gate，分别是输入门（input gate）、输出门（output gate）和遗忘门（forget gate），所以 LSTM 这种特殊的神经元有四个输入、一个输出：

所以，LSTM 的参数数量会比较多，是一般神经网络的 4 倍，LSTM 的训练会很难，并且 loss 的波动会很大，看起来会有点“异常”；还有因为在 LSTM 中网络是有记忆的，参数的扰动会带来很大的影响，有点类似蝴蝶效应，这也是造成 loss 波动大的原因之一。

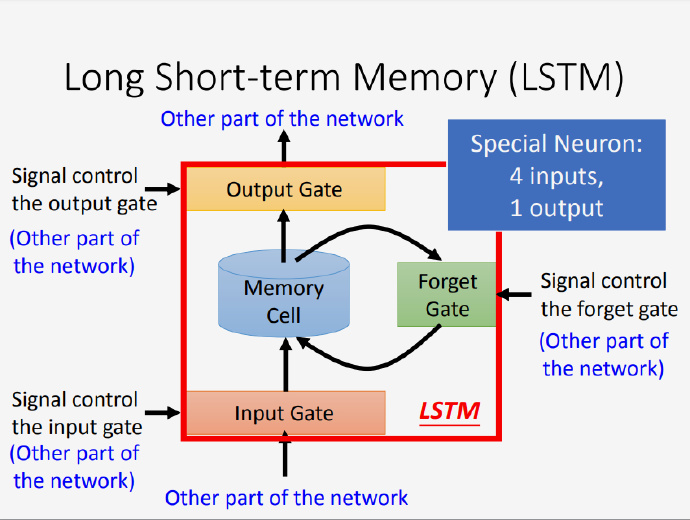
image

计算过程

下图是 LSTM 的计算过程，输入一共有四个：$Z$、输入门 $Z_i$、输出门 $Z_o$、遗忘门 $Z_f$，一个输出 $a$。三个门各司其职，每个门通常使用 sigmoid 函数作为激活函数，激活后的值处在 0 和 1 之间，故方便控制“门”的开启和关闭，输入门决定 $Z$ 能走多远，遗忘门决定记忆单元的值是否刷新或者重置，输出门则决定最后的能否被输出。

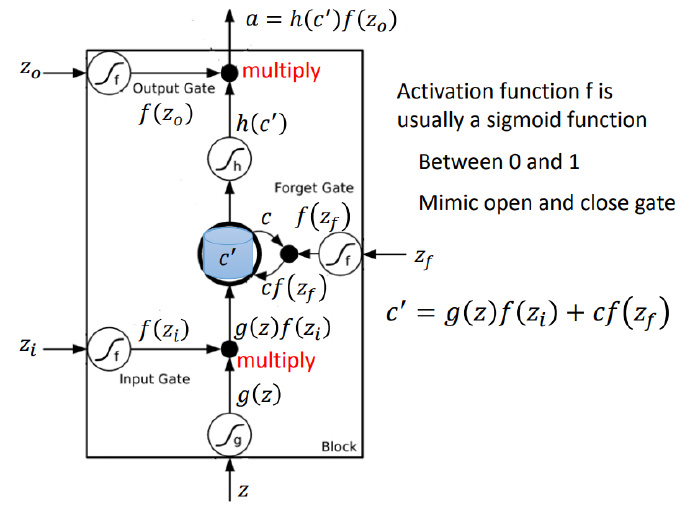
image

一个 LSTM 单元的计算过程如下：

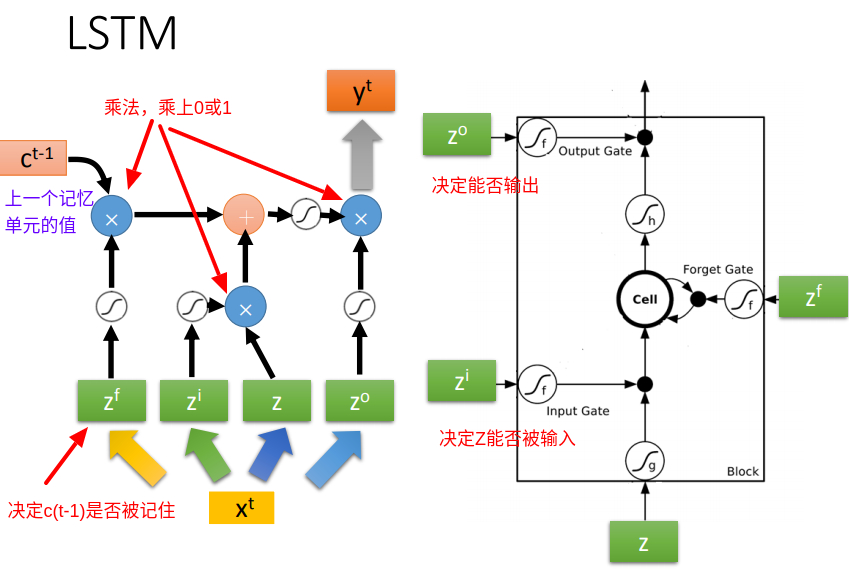
下图解释了在 LSTM 中上下文之间是如何关联起来的，每个输入 $x^{t+1}$ 都会接受来自上一个记忆单元的值 $c^t$

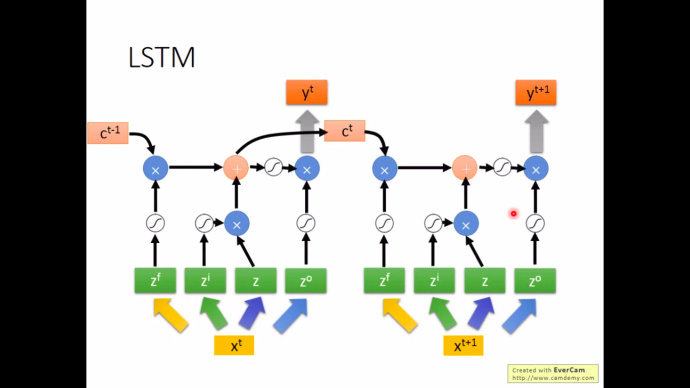
到此，LSTM 的基本知识学习完毕，总的来说，李宏毅老师的教学视频是目前为止最通俗易懂的，他的课程值得反复观看理解。当然，LSTM 的扩展千变万化，有多层、双向，LSTM 的参数多，实现起来比较困难，据说当时只有 mikolov 一个人的代码能 work。还好现在很多框架已经实现了这部分的工作，比如 keras、tensorflow 等等，直接拿过来用即可，这是我学完课程后，找了一些网上的代码做的一次 LSTM 文本分类实践：基于 Tensorflow 的 TextRNN 在搜狗新闻数据的文本分类实践 | Thinking Realm 。

最后引用一段话作为结尾：

不少搞工程的人认为，要理解什么东西，搞明白其底层数学描述是必要和充分的，你需要“了解背后的数学原理”。其实，在所有场景下，这几乎都不是充分的，也不是必要的——远远不是。以 PCA 为例，知道怎么做 5x5 矩阵对角化，算是“知道 PCA 背后的数学原理”。但这对你了解 PCA 是什么、能做什么，以及为何有用没太大帮助。你需要更高级的心智模式。 这几乎是普遍的事实：要理解某项事物，你需要正确的心智模式，抓住那些真正关键的方面，而不仅仅是最最底层的数学描述。大多数情况下，两种模式完全正交。深度学习反向传播也是如此——知道怎么写反向传播的程序，并不会让你了解深度学习的实用知识，相反，深入深度学习的心智模式，一定不是以了解反向传播算法细节为中心的。此外，有了正确的心智模式，在需要时可以很容易地自行得出算法细节，至少有效实现是没问题的。 via:François Chollet

参考资源

  1. 李宏毅老师的课件：Recurrent Neural Network (RNN)
  2. 李宏毅机器学习(2017)之RNN